 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел произведения равен произведению пределовСтр 1 из 6Следующая ⇒
Предел функции в точке. Единственность предела. Ограниченность функции, имеющей предел. Число А называется пределом функции f в точке а, если она определена на некоторой окрестности а, т.е. на некотором интервале (c,d), где c<a<d, за исключением, быть может, самой точки а, и если для всякого >0 можно указать зависящее от него >0 такое, что для всех x, для которых Теорема. Если Доказательство. Из условия теоремы следует существование окрестности U(a), такой, что Бесконечно малые функции.теорема о связи функции её предела и бесконечно малой.свойства бмф. Св-ва б.м.ф.: 1) Если функция f(x) ограничена, а m(x) бесконечно большая, то 2) Если абсолютная величина f(x) ограничена снизу положительным числом, а m(x) не равная нулю бесконечно мала, то Теорема.Если функция f(x) имеем предел,равный А,то её можно представить как сумму числа А и бесконечно малой функции α(x),т.е если Теорема (обратная).Если функцию f(x) можно представить в виде суммы числа А и бесконечно малой функции α(x) ,то число А является пределом функции f(x),т.е если f(x)=А+α(x),то Предел суммы равен сумме пределов:
Предел произведения равен произведению пределов
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b). Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b - a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.
3 Непрерывность функции в точке. Функция f(x) называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки, в том числе в самой точке х0, и если её приращение в этой точке, соответствующее приращению аргумента КОРОЧЕ: Теорема. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная Теорема. Пусть функции u=φ(х) непрерывна в точке х0, а функция у=ƒ(u) непрерывна в точке u0=φ(хо). Тогда сложная функция ƒ(φ(х)), состоящая из непрерывных, функций, непрерывна в точке х0. ТеоремаЕсли функция у=ƒ(х) непрерывна и строго монотонна на [a;b] оси (Oх, то обратная функция у=φ(х) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу. все основные элементарные функции непрерывны при всех значениях х, для которых они определены. Теорема о переходе к пределу под знаком непрерывной функции. Пусть ф-я y=f(x) непрерывна в x0. Это означает, что существует lim (x->x0) f(x) = p(x0). Пусть существует функция y=f(y) - непрерывная в y0 => p(x0)(lim(y->y0) f(y)) = f(y0). Тогда сложная функция y=f(p(x)) будет непрерывна в точке х, т.е предел сложной функции lim (x->x0) f[p(x)]=f(p(x0)]=f [lim (x->x0 p(x)]. Операция взятия предела и операция взятия непрерывности функции перестановочны между собой Теорема о непрерывности сложной функции. Пусть x = j(t) непрерывна в точке t0, а функция f(x) непрерывна в точке x0 = j(t0). Тогда функция y = f(j(t)) непрерывна в точке t0. Билет 4 Замечательные пределы Первый замечательный предел Предел Отношения синуса к его аргументу равен единице,когда аргумент стремится к нулю. Второй замечательный предел
Эквивалентные б.м.ф. Таблица эквивалентных б.м. Эквивалентными (асимптотически равными) называют функции j(x) и y(x) (обе стремящиеся к нулю), если выполняется свойство Теорема Предел отношения двух бесконечно малых функций не изменится,если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Билет 5 Если функции j(x )и y(x), участвующие в Теорема о связи ббф и бмф. Пусть функция f(x)-бб при Доказательство (?). Функция называется бесконечно большой при х-а, где а – число или одна из величин , ∞+∞ или
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)-0 при х-а (если х-∞ ) и не обращается в ноль, то
Билет 6 Односторонние пределы. Классификация точек разрыва. Число А называется пределом функции f(x) в точке x=a справа (при Точки, в которых функция f(x) не является непрерывной, называются точками разрыва для функции f(x). Если в точке x=a существуют пределы f(a+0), f(a–0), но неравенство Предел в бесконечности.Число А называется пределом функции к бесконечности если для любого положительного числа есущ такое число М=М(е)>0,что при всех x ,удовлетворяющих неравенству │Х│>М выполняется неравенство │f(x)-A│<e Геометрический смысл Для ¥е> 0 э м>0,что при Х €(-∞;-М) или (М,+∞) соответствующие значения функции f(x) попадают в е-окрестность точки А,т.е точки графика лежат в полосе шириной 2е,ограниченной прямыми y=A+e и y=A-e
7.билетПроизводная. Геометрический и механический смысл производной. Уравнение касательной и нормали к графику функции.
Геометрический смысл производной заключается в том, что есть tg угла наклона касательной, проведенной в точке x0. KN=Dy, MK=Dx tg угла KMN=Dy/Dx вычислим предел левой и правой части: limtga=lim(Dy/Dx) Dx®0 tga0=y` a®a0 При Dx®0 секущая MN®занять положение касательной в точке M(tga0=y`, a®a0). Касательной Т к кривой y=f(x), проходящей через точку (x;f(x)), называется предельное положение секущей при Dx®0. Уравнение касательной в точке M(x0,f(x0)) записывается в виде Нормалью к графику функции в точке M(x0,f(x0)) назовём прямую, проходящую через точку М и перпендикулярную касательной, проходящей через эту же точку.
8билет Дифференцируемость функции. Дифференциал. Необходимое и достаточное условие дифференцируемости. Геометрический смысл дифференциала. Функция f(x) называется дифференцируемой в точке х, если её приращение Теорема. Для того, чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она имела в этой точке конечную производную. Тогда величина А из Достаточность. Из существования производной выводим дифференцируемость
Поиск по сайту: |
 имеет место неравенство
имеет место неравенство  . Тот факт, что А есть предел f в точке a, принято записывать
. Тот факт, что А есть предел f в точке a, принято записывать  или
или 
 .
. , где A – конечное число, то на некоторой окрестности U(a) функция f(x) ограничена, т.е. существует положительное число М такое, что
, где A – конечное число, то на некоторой окрестности U(a) функция f(x) ограничена, т.е. существует положительное число М такое, что  для всех
для всех  ,.
,.
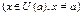 . Отсюда для указанных х
. Отсюда для указанных х  , где надо считать
, где надо считать  .
.

 =A,то f(x)=A+α(x).
=A,то f(x)=A+α(x). .
.

 , стремится к нулю при
, стремится к нулю при  :
:  .
. . Непрерывность основных элементарных функциий
. Непрерывность основных элементарных функциий

 .
. 
 , суть бесконечно малые при
, суть бесконечно малые при  , то j(x) при
, то j(x) при  есть бесконечно малая высшего порядка по отношению к (бесконечно малой) y(x) (если же это были бесконечно большие, то j(x) более низкого порядка, чем y(x).
есть бесконечно малая высшего порядка по отношению к (бесконечно малой) y(x) (если же это были бесконечно большие, то j(x) более низкого порядка, чем y(x). Бесконечно большая функция.
Бесконечно большая функция. , если , где А – число или одна из величин, или .
, если , где А – число или одна из величин, или .
 .
. не выполняется,
не выполняется,  то точка х=а называется точкой разрыва первого рода для функции f(x). Причём, если
то точка х=а называется точкой разрыва первого рода для функции f(x). Причём, если  , то точка x=a называется точкой устранимого разрыва для функции f(x). Если же в точке x=a у функции f(x) не существует правого или левого предела или же эти пределы бесконечны, то функция f(x) имеет в точке x=a разрыв второго рода.
, то точка x=a называется точкой устранимого разрыва для функции f(x). Если же в точке x=a у функции f(x) не существует правого или левого предела или же эти пределы бесконечны, то функция f(x) имеет в точке x=a разрыв второго рода. Производной функции f(x) в точке x называется предел её приращения
Производной функции f(x) в точке x называется предел её приращения  в этой точке к соответствующему приращению аргумента
в этой точке к соответствующему приращению аргумента  Определение записывается и таким образом
Определение записывается и таким образом 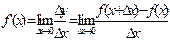 .
. .
. в этой точке может быть представлено в виде
в этой точке может быть представлено в виде  , где величина А не зависит от Dx.
, где величина А не зависит от Dx.