 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теория вероятностей и математическая статистика ⇐ ПредыдущаяСтр 10 из 10
Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид
где а – математическое ожидание, σ – среднее квадратическое отклонение Х. Вероятность того, что Х примет значение, принадлежащее интервалу (α,β), Р(α<х<β)=Ф где Ф(х)=
Пример 1.Математическое ожидание а нормально распределенной случайной величины Х а=10, среднее квадратическое отклонение σ=2. Найти вероятность попадания этой величины в интервал (12;14). Решение: Подставив в формулу (1) α=12, β=14, а=10, σ=2, получаем Р(12<х<14)=Ф По таблице для функции Лапласа находим, что Ф(2)= 0,4772, Ф(1)=0,3413 и искомая вероятность Р(12<х<14)=0,1359. Оценки, которые определяются одним числом, называют точечными. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать этих ошибок, используют интервальные оценки, которые определяются двумя числами – концами интервала (в котором заключена оцениваемая величина с заданной вероятностью). Таким образом, задача сводится к отысканию такого интервала (его называют доверительным), который с заданной вероятностью γ (ее называют надежностью) покрывают оцениваемый параметр. Наиболее часто надежность принимают равной 0,95 или 0,99, или 0,999. В частности, при надежности γ=0,95 доверительный интервал для оценки математического ожидания а нормального распределения (по выборочной средней
В обозначениях формула принимает вид: Если доверительный интервал найден, то с надежностью 0,95 можно считать, что оцениваемый параметр заключен в этом интервале. Пример 2.Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю Решение: Воспользуемся формулой:
Подставляя данные, получаем: 10,43-1,96(5/10)<а<10,43+1,96(5/10), или окончательно 9,45<а<11,41. Контрольные задания
Ниже приведена таблица номеров задач, входящих в задания на контрольные работы. Студент выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра. При этом если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в табл. 1; если же предпоследняя цифра учебного шифра есть число четное или ноль (2, 4, 6, 8, 0), то номера задач для соответствующего варианта даны в табл.2 Таблица 1
Таблица 2
Номера задач для первого курса бакалавриата: 21-40, 61-80, 101-120, 161-180, 191-210, 231-240, 251-260
Номера задач для второго курса бакалавриата: 261-280, 291-320, 341-360, 361-370, 411-430, 491-520
Номера задач для первого курса магистратуры: 441-460, 461-480 ЛИТЕРАТУРА
1. Клетеник Д.В. «Сборник задач по аналитической геометрии» - М., Гостехиздат, 1954-1956 гг.; М., Физматгиз, 1958-1963 гг.; М., Наука, 1965-1980 гг. 2. Пискунов Н.С. «Дифференциальное и интегральное исчисления для вузов» - М., Наука, 1970-1978 гг., т. 1, 2. 3. «Задачи и упражнения по математическому анализу для вузов» / Под ред. Б.П. Демидовича – М., Физматгиз, 1959-1963 гг.; М., Наука, 1964-1978 гг. 4. Моисеенко А.М., Александрова Е.В. «Линейная алгебра». 5. Уварова М.Н., Александрова Е.В. «Теория вероятности».
Поиск по сайту: |
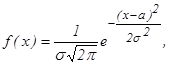
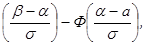 (1)
(1)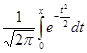 - функция Лапласа.
- функция Лапласа.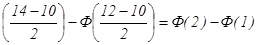
 выборки объема n, при известном σ) находят по формуле
выборки объема n, при известном σ) находят по формуле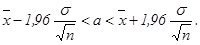

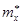 ), объем выборки (число наблюдений) n=100 и среднее квадратическое отклонение σ=5.
), объем выборки (число наблюдений) n=100 и среднее квадратическое отклонение σ=5.