|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Элементы операционного исчисления
Пусть функция f(x) обладает следующими свойствами: 10. f(x) ≡0 при t < 0. 20. |f(x)| < МеSot при t > 0 , где М > 0 и S0 – некоторые действительные постоянные. 30. На любом конечном отрезке [а, в] положительной полуоси Ot функция f(x) удовлетворяет условием Дирихле, т.е.: а) ограниченна; б) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода; в) имеет конечное число экстремумов. Такие функции в операционном исчислении называются изображаемыми по Лапласу, или оригиналами. Пусть р = α + βi - комплексный параметр. При сформированных условиях интеграл
Этот интеграл называется интегралом Лапласа, а определяемая им функция комплексного аргумента р называется преобразованием Лапласа от функции f(t) или лапласовым изображением f(t) или просто изображением f(t) .
Таблица изображений основных элементарных функций
Тот факт, что функция Если дано линейное дифференцированное уравнение n-го порядка с постоянными коэффициентами y(n) + a1y(n-1) +…+ any = f(t),
правая часть которого f(t) является оригиналом, то и решение этого уравнения, удовлетворяющее произвольным начальным условиям вида:
y (0) = y0, у΄(0) = y΄0 , y΄΄=y0΄΄, … ,y(n-1)(0) = y(n-1)0
(т.е. решение задачи Коши, поставленной для этого уравнения, с начальными условиями при t = 0, служит оригиналом. Обозначая изображение этого решения через Пусть оригинал f(t) дифференцируем n раз и его производные до n-го порядка в свою очередь являются оригиналами. Тогда справедлива теорема дифференцирования оригинала: если f(k)(t) В частности : f΄ f΄΄(t) f΄΄΄(t) Пример 1. Решить дифференциальное уравнение
y΄΄΄-6y΄΄+11y΄-6y=0, если у(0) = 0, у΄(0) = 1, у΄΄(0) = 0. Решение. Переходя к изображениям по теореме дифференцирования оригинала, получим:
Используем элементарные приемы для разложения этой дроби на сумму, таких простейших дробей, оригиналы которых известны:
Полагая р=1, находим –5 = 2А, откуда А = -5/2. Полагая р=2, находим –4 = -В, откуда В = 4. При р = 3, находим –3 = 2С, откуда С = -3/2.
Следовательно,
Отсюда, используя формулу (3) таблицы изображений, находим:
Пример 2. Решить систему уравнений: Решение. Перейдем к изображениям:
х΄
Система уравнений примет вид:
Из первого уравнения системы выразим
Выразим из 2-го уравнения
Осталось найти оригинал для
Полагая р =-1 получаем –8 = 4В, откуда В= -2. Полагая р = 0, получаем 2 = -3А, откуда А =- Полагая р = 3, получаем 32 = 12 С, откуда С = Следовательно:
Тогда Аналогично поступим с дробью для отыскивания оригинала для
При р = -1, 8 = 4В, откуда В = 2. При р = 0, -1 = -3А, откуда А = При р = 3, получаем 32 = 12 С, откуда С = Следовательно:
Тогда
Пример 3. Решить дифференциальное уравнение методом операционного исчисления
у΄΄-2у΄-3у = е3t, если у(0) = 0, у΄(0) = 0. Решение Перейдем к изображениям:
y΄΄ y΄ y е3t
или, учитывая начальные условия:
квадратный трехчлен р2- 2р – 3 можно разложить на два множителя, так как его корни р1= 3, р2 = -1: р2 – 2р – 3 = (р -3)(р+1). Окончательно имеем:
Полагая р = -1, получаем 1 = 16С, т.е. При р = 3, имеем 1 = 4А, т.е. Сравнивая коэффициенты при р2, получим О = В +С, т. е.
откуда, используя таблицу изображений, находим искомый оригинал и решение данного дифференциального уравнения:
или
Пример 4. Решить систему уравнений: Решение. Перейдя к изображениям имеем:
Из 1-го уравнения системы выразим
Из 2-го уравнения системы выразим
Таким образом:
Таким образом:
Разложив, полученные дроби на простейшие, по таблице изображений найдем оригинал:
При р = 5 : 12 = 10А, А = 1, 2. При р =5 : 6 = 10С, С = 0,6. При р = -5 : 2 =-10В, В = -0,2. При р = -5 : -4 = -10Д, Д = 0,4.
Следовательно,
Откуда
Поиск по сайту: |
 сходится и является функцией от р.
сходится и является функцией от р.
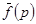




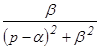

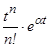






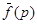 является изображением оригинала f(t), обозначается следовательно символом
является изображением оригинала f(t), обозначается следовательно символом  f(t).
f(t). , находим изображение левой части исходного дифференцированного уравнения и, приравнивая его к изображению функции f(t) ,приходим к так называемому изображающему уравнению, которое всегда является линейным алгебраическим уравнением относительно
, находим изображение левой части исходного дифференцированного уравнения и, приравнивая его к изображению функции f(t) ,приходим к так называемому изображающему уравнению, которое всегда является линейным алгебраическим уравнением относительно  f(t), то
f(t), то pk
pk  p ·
p · 
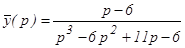 или
или
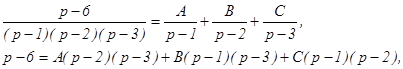


 если х(0) =0, у (0) = 5.
если х(0) =0, у (0) = 5.
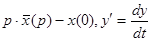
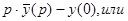



 , подставим во 2-ое уравнение:
, подставим во 2-ое уравнение:
 или
или


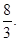
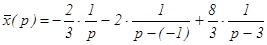 .
.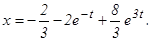
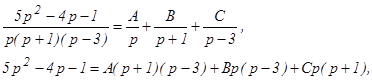
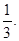




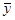
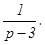 Тогда данное дифференциальное уравнение примет вид:
Тогда данное дифференциальное уравнение примет вид:
 откуда
откуда
 Осталось найти оригинал данной функции. Разложим полученную рациональную дробь на простейшие дроби:
Осталось найти оригинал данной функции. Разложим полученную рациональную дробь на простейшие дроби:
 ;
;
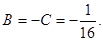 Следовательно,
Следовательно,
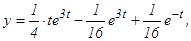

 если х(0) = у (0) =1.
если х(0) = у (0) =1.



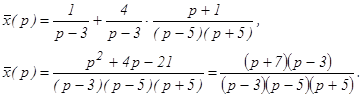



 и
и