 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
V. Неопределенный и определенный интегралы
Для справок приводим таблицу неопределенных интегралов. Интегрирование, основное на применение таблицы основных интегралов, основных свойств неопределенного ∫ - ла, а также простейших тождественных преобразований подынтегральной функции, принято называть непосредственным интегрированием. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
Пример 1. Найти интегралы: а) Решение. а) Применяя табличные интегралы, получим:
б) Преобразуем подынтегральную функцию и представим заданный интеграл в виде суммы двух других, каждый из которых табличный:
в) Чтобы привести данный интеграл к табличному, выразим стоящую в числителе единицу как sin2x + cos2x и разделим почленно на знаменатель:
Если данный интеграл
Пример 2. Найти интегралы, применяя соответствующие подставки: а)
Решение. а) Чтобы привести данный интеграл к табличному, положим t = x2 + 1. Дифференцируя, получим dt = 2xdx, xdx =
б) Пусть t = arcsin x, тогда
в) Так как cosxdx есть дифференциал функции sin x, то данный интеграл приводится к табличному так:
Пусть u и d (u Проинтегрировав обе части последнего равенства, получим:
Эта формула (1) называется формулой интегрирования по частям. Ей пользуются в тех случаях, когда
Пример 3. Найти интегралы: Решение. а) Пусть u = х и dσ = e2xdx, тогда du = dx и σ = Произвольную постоянную С можно учесть в окончательном ответе. Применяя (1), получаем:
б) Пусть u = arc sin x, dσ = dx, тогда
+
Интегрирование рациональных дробей Рациональной дробью называется дробь вида Простейшими (элементарными) дробями называются правильные дроби следующего вида:
I. III. IV. Во всех четырех случаях предполагается, что А, В, р, q, а – действительные числа. Перечисленные дроби соответственно называют соответственно дробями I, II, III и IV типов. Рассмотрим интегралы от простейших дробей I, II, III типов: I. II. III. IV.
Пример 4. Найти интегралы:
Решение. а) Данная дробь – правильная, ее знаменатель разложен на простейшие множители. Множителю (х – 1)3 соответствует сумма трех простейших дробей
Освободимся от знаменателя: х2 + 1 = А(х + 3) + В(х – 1)2(х + 3) + С(х – 1)2(х+3)+ D(x – 1)3 (*)
Действительными корнями знаменателя являются числа 1 и –3. Полагая в (*) х = 1, получаем, что 2 = 4А или А= Полагая в (*) х = -3, получаем, что 10 = - 64 D или D = Сравним теперь коэффициенты при старших степенях х в левой и правой частях (*), т.е. при х3. В левой части равенства (*) нет члена с х3, т.е. коэффициент при х3 равен 0. В правой части коэффициент при х3 равен С + D. Итак, С + D = 0, откуда C = Остается определить коэффициент В. Для этого надо иметь еще одно уравнение. Это уравнение можно получить путем сравнения коэффициентов при одинаковых степенях х (например, при х2) или придав х какое-нибудь числовое значение. Удобнее взять такое значение, при котором вычислений будет возможно меньше. Полагая х = 0, получаем из равенства (*): 1 = 3А – 3В + 3С – D или Окончательное разложение данной дроби на простейшие имеет вид:
Таким образом, получим:
б) Разложим знаменатель дроби на множители: х5 – х2 = х2(х3 - 1) = х2(х – 1) (х2 + х + 1). Тогда
Освобождаемся от знаменателя: 1 = А(х – 1)(х2 +х + 1) + В(х – 1)(х2 + х + 1)х + С х2(х2 + х + + 1) + (Dx + E) x2 (x – 1). Действительными корнями знаменателя являются числа 0 и 1. Из последнего равенства при х = 0 имеем 1 = -А, т.е. А = -1; при х = 1, имеем 1 = 3С, т.е. С = Перепишем предыдущее равенство в виде: 1 = А(х3 – 1) + В(х4 – х) + С(х4 + х3 + х2) + Dx4 +Ex3 –Dx3 – Ex2. Сравнивая коэффициенты при х4, х3, х2, получаем систему уравнений
Итак, Следовательно,
в) Так как х2 + 1 есть двукратный множитель, то
х3 : 1 = С, х2 : 0 = D, х : -2 = А + С, А = -3, х0 : 0 = В + D, В = 0.
Следовательно,
г) Выделим целую часть данной неправильной дроби, поделив числитель на знаменатель:
Следовательно, Разложим теперь правильную дробь на простейшие дроби:
Освободимся от знаменателей: 8х3 – 16х + 1 = А(х + 2)2+ В(х – 2)(х + 2)2+С(х – 2)2+D(х + 2)(х – 2)2. Принимая в последнем равенстве: х = 2 : 33 = 42 А, откуда А= х = -2 : -31 = 16 С, откуда С= - х =0 : 1 = 4А – 8В + 4С + 8D, откуда –16В + 16D = 1. Для того, чтобы найти В и D, сравнив коэффициенты при х3, получим еще одно уравнение: 8 = В + D. Решим получившуюся систему уравнений: Находим, что Итак, Пример 5. Вычислить приближенное значение определенного интеграла Решение. Приближенные методы интегрирования имеют очень большое значение. На практике часто приходится иметь дело с определенными интегралами, которые с помощью формулы Ньютона – Лейбница или искусственными приемами найти практически невозможно. В этом случае значение интеграла
где n – четное число, на которое разбивается отрезок интегрирования, В данном примере n = 10, а = 2, в = 12, то
Составим таблицу значений данной функции
4 411,696
80,147
2 160,294.
Окончательно получаем: Несобственные интегралы Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций.
Несобственный интеграл от функции f(x) в пределах от а до + ∞ определяется равенством:
Если этот предел существует и конечен, то несобственный интеграл (3) называется сходящимся; если же предел не существует или равен бесконечности – расходящимся. Аналогично:
Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a; в] и непрерывна при а ≤ х <с и с < х ≤ в, то по определению полагают:
Несобственный интеграл
Пример 6. Вычислить несобственные интегралы или установить их расходимость:
а) Решение. а) Применяя равенство (3), получаем:
следовательно, рассматриваемый несобственный интеграл расходится.
б) Применяя равенство (4), получаем:
в) Подынтегральная функция
Применяя равенство (6), получаем:
следовательно, данный интеграл сходится и он равен 6.
Определенный интеграл Пример 7. Найти площадь фигуры, ограниченной параболой Решение. Площадь фигуры, ограниченной сверху непрерывной кривой у = f(x), снизу – непрерывной кривой у = φ(х), слева – прямой х = а, справа – прямой х = в, вычисляется по формуле
Определенный интеграл вычисляется по формуле Ньютона – Лейбница:
для которого необходимо найти первообразную функцию F(x) и вместо переменной х подставить сначала верхний предел в, затем нижний предел а и из 1-го результата вычесть второй.
Определим точки пересечения данных линий, решив совместно систему уравнений
Подставив в 1-ое уравнение системы суммы (х + 1), вместо у, получим:
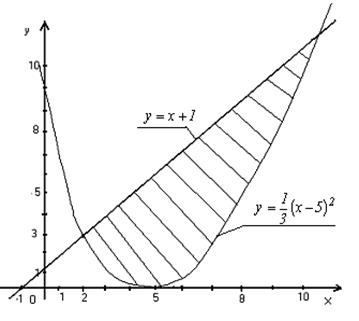
откуда х1 = 2, х2 = 11 и, следовательно, у1=3, у2=12.Таким образом, парабола и прямая пересекаются в точках А(2; 3) и В(11; 12) (рис. 10).
Так как сверху фигура ограниченна прямой, а снизу – параболой, то применяя формулу (7), имеем:
Рис. 10 Дифференциальные уравнения (ДУ)
ДУ І порядка имеет вид: F = ( x, y, y/) (1)
или (если его можно разрешить относительно у/) вид:
у/ = f (x, y) (2)
Решение уравнения (1) или (2), содержащее произвольную постоянную С, то есть имеющее вид у = φ (х, С), называется общим решением этого уравнения. Если это решение получается в неявной форме Ф (х, у, С) = 0, то его называют общим интегралом уравнения (1) или (2). Если придать произвольной постоянной С некоторое фиксированное значение, то из общего решения (общего интеграла) получим частное решение (частный интеграл) этого уравнения. Уравнение І порядка Р (х, у) dx + Q (x, y) dy = 0 называется уравнением с разделяющимися переменными, если функция Р (х, у) и Q (х, у) разлагаются на множители, зависящие каждый только от данной переменной:
f1 (x) f2 (y) dx + φ1 (x) φ2 (y) dy = 0 (3)
В этом уравнении путем деления его членов на f2 (y)φ1 (x) переменные разделяются и общий интеграл находится почленным интегрированием:
Функция f(x, y) называется однородной измерения m, если f (λ x, λy) = λm f(x, y). Однородное ДУ первого порядка называется уравнение у/ = f (х,у), если f(х,у) – однородная функция нулевого измерения. Замечание. Уравнение вида P(x,y)dx + Q(x,y)dy = 0 будет однородным, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения. Однородное уравнение может быть приведено к виду у/ = f(y/x). С помощью подстановки у/х = t однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции t = t(x). Уравнение вида:
где Р (х) и Q (x) – заданные непрерывные функции, называются линейным. ДУ І порядка (у и у/ входят в первых степенях, не перемножаясь между собой). Если Q (x) ≠ 0, то уравнение называется линейным неоднородным, а если Q = 0 – линейным однородным в смысле правой части. Неоднородное линейное ДУ І порядка посредством замены искомой функции у = иσ сводится к двум уравнениям с разделяющимися переменными относительно каждой из вспомогательных функций.
Пример 1. Найти общее решение ДУ.
а) б) Решение. а) Данное уравнение является однородным, так как функции Р(х, у)=2ху и Q(х, у)=(у2-х2) – однородные второго измерения относительно х, у:
Применяем подстановку у = хt, где t – некратная функция аргумента х. Если у = хt, то дифференциал dy = tdx + xdt, и данное уравнение примет вид:
2х . xtdx + (x2t2 – x2) (tdx + xdt) = 0
Сократив на х2, будем иметь:
Получилось уравнение с разделенными переменными относительно х и t. Интегрируя, найдем общее решение этого уравнения:
Потенцируя, находим
б) Поделим обе части уравнения на произведение функции ху, получим:
Введем подстановку
Разделяя переменные и интегрируя, имеем:
Возвращаясь к переменным х и у, получаем
Пример 2. Решить уравнение.
а) б) Решение. а) Поделим обе части уравнения на соs х:
Это линейное неоднородное уравнение. Введем подстановку у = иσ, тогда у΄= и΄σ + иσ΄ и данное уравнение (1) преобразуется к виду
Так как искомая функция у представлена в виде произведения двух вспомогательных функций и и σ, то одну из них можно выбрать произвольно. Выберем в качестве σ какой-либо частный интеграл уравнения:
Тогда для отыскивания функции и получим уравнение:
Уравнение (2), есть уравнение с разделяющимися переменными относительно σ и х. Решим его:
Чтобы равенство (2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрирования находим то частное решение, которое соответствует значению произвольной постоянной С=0. Подставив в (3) найденное выражение для σ, получим:
Интегрируя, получаем:
Тогда
б) Данное уравнение является линейным, так как оно содержит искомую функцию у и ее производную у/ в первой степени и не содержит их произведений. Применяем подстановку
Полагаем u΄-utg x = 0 (5)
Тогда уравнение (4) примет вид:
Уравнение (5) – уравнение с разделяющимися переменными. Решим его:
(значение произвольной постоянной принимаем С=0)
Подставив в (6) найденное выражение для и, получим:
Тогда
Дифференциальным уравнением n-го порядка называется уравнение вида: F(x, y΄y΄΄,…y(n)) = 0 Решением такого уравнения служит всякая n раз дифференцированная функция у = φ (х), которая обращает данное уравнение в тождество, т.е.:
F (x, φ(x), φ΄(x), φ(n)(x)) = 0. Для дифференцированного уравнения вида
F (x, y(k), y(k+1), … , y(n))= 0, Не содержащего искомой функции у, порядок уравнения можно понизить, взяв за новую неизвестную функцию низшую из производных данного уравнения, т.е. пологая y(k)=z. Тогда получим уравнение F (x, z, z΄, … , z(n-k)) = 0 Таким образом, порядок уравнения понижается на k единиц.
Пример 3. Найти общее решение уравнения
Решение. Данное уравнение II порядка не содержит явно функцию у. Положим у΄=z, где z – некоторая функция аргумента х. Если у΄=z, то у΄΄=z΄ и данное уравнение (1) примет вид:
Это однородное уравнение I порядка. Введем подстановку
Интегрируя, находим:
Потенцируя, получаем:
Возвращаясь к переменной у, приходим к уравнению Это уравнение вида у(n)=f(x), решение которого находится n – кратным интегрированием. Следовательно,
Положим u = x, dσ=
Для ДУ вида F (y, y΄, y΄΄, … , y(n)) = 0, не содержащего независимой переменной х, допускается понижение порядка на единицу, если положить у/ = z, а за новый аргумент принять сам у. В этом случае у΄΄, у΄΄΄, … выразятся по формулам (они выводятся по правилу дифференцирования сложной функции:
Пример 4. Решить уравнение у΄΄(1 + у) = у΄2+ у΄. Решение. Уравнение не содержит независимой переменной х. Положим у΄= z, y΄΄=
Возвращаясь к переменной у, получаем уравнение у΄=С1(у + 1) – 1; это уравнение I порядка с разделяющимися переменными.
Линейные неоднородные дифференциальные уравнения II порядка с постоянными коэффициентами.
Уравнение где p и q – действительные числа, f(x) – известная непрерывная функция, называется линейным неоднородным дифференциальным уравнением II порядка с постоянным коэффициентом. Функция y=φ(x, C1, C2), удовлетворяющая уравнению (1) при любых значениях произвольных С1 и С2, называется его общим решением. Решение уравнения (1), получающиеся из общего решения при конкретных значениях постоянных С1 и С2, называется частным решением уравнения (1). Т.к. в функцию y=φ(x, C1, C2) входят две произвольные постоянные C1 и C2; то для выделения из общего решения уравнения (1) некоторого частного решения необходимо иметь два начальных условия: если х=х0, то у=у0, у′= у′0, то есть у(х0)=у0, у′(х0)= у′0.. Для общего решения неоднородного уравнения (1) справедлива следующая теорема.
ТЕОРЕМА. Общее решение уоб.н. неоднородное уравнение (1) равно сумме общего решения уодн соответствующего однородного уравнения уоб.н.=уодн+уч.н. Согласно этой теореме для решения уравнения (1) вначале находится функция уодн – решение однородного дифференциального уравнения
где p, q – постоянные действительные числа. Общее решение уравнения (2) находится с помощью характеристического уравнения.
k²+pk+q=0, (3)
которое получается из уравнения (2), если, сохраняя в нем коэффициенты p и q, заменить функцию у′ единицей, а все ее производные соответствующими степенями k. При этом: 1) Если корни k1 и k2 характеристического уравнения (3) действительные и различные, то общее решение уравнения (2) выражается формулой
2) Если корни k1 и k2 характеристического уравнения (3) действительные и равные (k1=k2), то общее решение уравнения (2) выражается формулой
3) Если корни k1 и k2 характеристического уравнения (3) комплексные(k1=α+βi, k2= α-βi), то общее решение уравнения(2) есть:
Для некоторых специальных видов функции f(x) частное решение уч.н. уравнение (1) можно найти методом неопределенных коэффициентов. По виду правой части f(x) можно заранее указать вид частного решения уч.н., где неизвестны лишь числовые коэффициенты, в следующих простейших случаях.
I. f(x)=Pn(x), где Pn(x) – многочлен степени n. В этом случае уч.н. есть многочлен Qn(x) той же самой степени n,что и многочлен Pn(x), если число 0 не является корнем характеристического уравнения (3); если же число 0 является корнем характеристического уравнения кратности r, то уч.н.=хкQn(x).
II. f(x)=aemx (a, m – некоторые числа). В этом случае уч.н.=Аеmx, если число m не является корнем характеристического уравнения (3) и уч.н.=Аxrеmx, если число m является корнем характеристического уравнения кратности r. Здесь А – подлежащий определению коэффициент.
III. f(x)=emx Pn(x), где Pn(x) – многочлен степени n. В этом случае уч.н.=еmxQn(x), если число m не является корнем характеристического уравнения и уч.н.=хrеmxQn(x), если число m является корнем характеристического уравнения кратности r. Здесь Qn(x) – многочлен той же степени n, что и Pn(x). Например: Q0(x)=А; Q1(x)=Ах+В; Q2(x)=Ах2+Вх+С; Q3(x)=Ах3+Вх2+Сх+D; и т.д. Коэффициенты А,В,С,D подлежат определению.
IV. f(x)=eαx(acosβx+bsinβx). Тогда уч.н.=еαx(Аcosβx+Вsinβx), если число α±βi не является корнем характеристического уравнения и уч.н.=хеαx(Аcosβx+Вsinβ x), если число α±βi является корнем характеристического уравнения. Здесь А и В - подлежащие определению коэффициенты.
V. Правая часть уравнения (1) функция f(x) есть сумма указанных функций. Тогда частное решение уч.н. этого уравнения есть сумма частных решений уравнений с той же левой частью, что и уравнение (1), а правые части этих уравнений есть каждое слагаемое правой части уравнения (1).
Пример 5. Найти частное решение дифференциального уравнения
а) y″-2y′+10y=6cos2x+4sin2х, y(0)=1,y′(0)=6; б) y″-9y′8y=3x2+2x+1, y(0)= Решение: а) Вначале находим общее решение однородного уравнения y″-2y′+10y=0; соответствующего данному неоднородному уравнению. Составим и решим его характеристическое уравнение. k2-2k+10=0 D=4-4·1·10=-36<0, значит, уравнение имеет два комплексно-сопряженных числа.
Тогда общее решение соответствующего однородного уравнения будет (согласно п.3). уодн=ex(C1cos3x+C2sin3x). Правая часть данного уравнения f(x)=6cos 2x+4sin2x, где по п. IV α=0, a=6, b=4, β=2 и числа α±βi =±2i не является корнем характеристического уравнения. Тогда частное решение данного неоднородного уравнения будет функция вида уч.н.=е0x(Аcos 2x+Вsin2x)= Аcos 2x+Вsin2x. Найдем производные первого и второго порядка функции уч.н.: y′ч.н.=-2Asin2x+2Bcos2x, y″ч.н=-4Acos2x-4Bsin2x. Представим уч.н, y′ч.н, y″ч.н в данное неоднородное уравнение: -4Acos2x-4Bsin2x-2(.-2Asin2x+2Bcos2x)+10(Аcos 2x+Вsin2x)= 6cos2x+4sin2x, (6А-4В)cos 2x+(6B+4A)sin2x=6cos 2x+4sin2x, которое будет тождеством только при равенстве коэффициентов у подобных членов в обеих его частях:
Следовательно, уч.н=cos 2x и общее решение данного неоднородного уравнения будет: уоб.н.=уодн+уч.н., уоб.н= ex(C1cos3x+C2sin3x)+ cos 2x Используя начальные условия, найдем значения произвольных постоянных С1 и С2. Подставляя в общее решение заданные значения х=0, у=1 (первое начальное условие), получим 1= e0(C1cos0+C2sin0)+ cos 0 или 1=С1+1, С1=0. Дифференцируем общее решение: у′= ex(C1cos3x+C2sin3x)+ ex(-3C1sin3x+3C2 cos3x)-2sin2x или у′= ex((C1+3C2 )cos3x+(C2-3C1)sin3x)-2sin2x Подставим в результат дифференцирования заданные значения х=0 и у′=6 (второе начальное условие), получим второе уравнение с неизвестными С1 и С2: 6= e0((C1+3C2 )cos0+(C2-3C1)sin0)-2sin2x или С1+3С2=6. Решая полученные уравнения как систему, найдем С1=0 и С2=2. Подставляя значения С1=0, С2=2 в общее решение, получим искомое частное решение, удовлетворяющее заданным начальным условиям. у=2ехsin3x+cos2x. б) Составим однородное уравнение, соответствующее данному неоднородному
Его характеристическое уравнение k²-6k+8=0 имеет корни k1=2, k2=4, поэтому общее решение соответствующего однородного уравнения будет уодн=C1е2х+С2е4х. Теперь находим частное решение уч.н. данного неоднородного уравнения. Для правой части данного уравнения f(x)=3x2+2x+1. Число 0 не является корнем характеристического уравнения, поэтому уч.н. есть многочлен той же степени, что и f(x), т.е. многочлен второй степени уч.н.=Ах2+Вх+С. Отсюда, дифференцируя, находим у′ч.н.=2Ах+В, у″ч.н.=2А и подставляя уч.н., у′ч.н. и у″ч.н. в данное уравнение, получим равенство 2А-6(2Ах+В)+8(Ах2+Вх+С)=3х2+2х+1, 2А-12Ах+6В+8Ах2+8Вх+8С=3х2+2х+1, 8Ах2+(8В-12А)х+(8С-6В+2А)=3х2+2х+1. Приравнивая коэффициенты при одинаковых степенях х из обеих его частей, а только при этом условии оно будет тождественным, получим систему:
Следовательно, уч.н.=С1е2х+С2е4х+ уч.н.=С1е2х+С2е4х+ Используя начальные условия, найдем значения произвольных постоянных С1 и С2. Подставляя в общее решение первое начальное условие (х=0, у= С1+С2+ Дифференцируя общее решение у′=2С1е2х+4С2е4х+ и подставляя в результат второе начальное условие(х=0, у′= 2 С1+4С2+ Решив полученные уравнения как систему, найдем С1 и С2:
Подставляя значения С1=2, С2=-1 в общее решение получим искомое частное решение, удовлетворяющее заданным начальным условиям: у=2е2х-е4х+
Линейные однородные системы ДУ с постоянными коэффициентами. Пусть данная система n-линейных ДУ с n неизвестными функциями, коэффициенты которой постоянные:
Эту систему можно записать в виде одного матричного уравнения:
Здесь
Ищем решение системы в виде: х1=р1еλt, х2 = р2еλt, … , хn=pneλt, где λ = const, pi=const (i = 1, 2, …, n).
Подставив значения х1, х2, …, хn в систему ДУ, получим систему линейных алгебраических уравнений относительно р1, р2, … , рn:
Система должна иметь ненулевое решение, поэтому для определения λ получаем уравнение n-ой степени, которое является характеристическим уравнением системы:
Предположим, что характеристическое уравнение имеет n различных корней λ1, λ2, … , λn , которые являются характеристическими числами матрицы А. Каждому характеристическому числу λk соответствует свой собственный вектор (р1k, p2k, … , pnk), где k = 1, 2, 3, … , n. Тогда система ДУ имеет n решений.
1-ое решение, соответствующее корню 2-ое решение, соответствующее корню ……………………………………………………………………………………………………….. n-ое решение, соответствующее корню
Мы получили фундаментальную систему решений. Общее решение системы таково:
Пример 6. Найти общее решение системы ДУ Решение. Запишем данную систему ДУ в виде матричного уравнения: где
Составим характеристическое уравнение матрицы системы:
Корни характеристического уравнения λ1= 1, λ2= 10 – характеристические числа матрицы. При λ1= 1, уравнение для определения собственного вектора имеет вид При λ = 10, получаем уравнение
для λ = 1 : х11 = еt , х21= -2еt; для λ= 10 : х12 = е10t, x22=e10t. Общее решение системы имеет вид:
x = C1x11+C2x12, x = C1et + C2e10t, y = C1x21 + C2x22, y = -2C1et + C2e10t. Кратные, криволинейные и поверхностные интегралы. Площадь плоской фигуры, ограниченной областью D, находится по формуле:
Если область D определена, например, неравенствами а≤x≤b, φ1(х)≤y≤φ2(х), то
Если область D в полярных координатах определена неравенствами α≤θ≤β, φ(θ)≤ρ≤f(θ), то
Преобразование прямоугольных координат х, у к полярным координатам ρ, θ, осуществляется по формулам х=ρcosθ, y= ρsinθ, где ρ – полярный радиус – вектор произвольной точки М, θ – полярный угол точки М.
Пример 7. Найти площадь фигуры, ограниченной кривой:
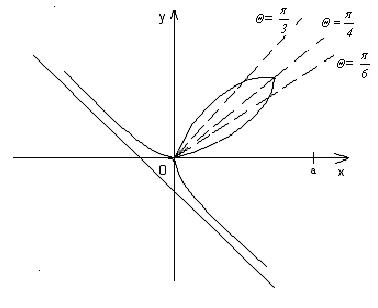
а) (х2+у2)=2а2ху (лемниската) б) х3+у3=аху (площадь петли).
Решение: а) Полагая х=ρcosθ, y=ρsinθ, преобразуем уравнение кривой к полярным координатам. В результате получим:
(ρ2cos2θ+ ρ2sin2θ)2=2а2ρ2cosθsinθ или ρ2=2а2cosθsinθ=а2sin2θ.
Построим кривую. Разрешив уравнение относительно ρ, находим ρ=±а
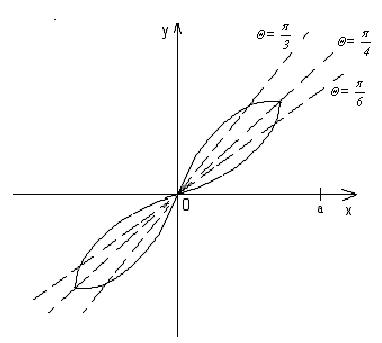
Исследуем форму лемнискаты для I четверти, т. е. для случая ρ≥0, 0≤θ≤π∕2. Для этого составим таблицу, учитывая, что ρ=±а
Построим данную кривую.
Нетрудно заметить, что θ может измениться только в промежутке от 0 до
Т.о., площадь искомой фигуры S=a2 кв.ед.
б) х3+у3=аху Преобразуем данное уравнение к полярным координатам ρ3(sin3θ+cos3θ)=aρsinθcosθ, т.е.
Построим петлю в I четверти, т.е. ρ>0, 0≤θ≤π/2.
Составим таблицу значений.
Осью симметрии петли является луч θ=
Т.о., площадь петли S= Числовые ряды Пусть и1, и2, … , иn, …, где иn= f(n) – бесконечная числовая последовательность. Выражение
и1+ и2+ и3 + …+ иn+ … называется бесконечным числовым рядом, а числа и1, и2 , … , иn – членами ряда ; иn = f(n) – называется общим членом. Ряд часто записывают в виде: Перечислим важнейшие признаки сходимости и расходимости рядов с положительными членами. Необходимый признак сходимости ряда. Если ряд и1+ и2+ и3 + …+ иn+ … сходится, то Первый признак сравнения. Пусть даны два ряда
и1+ и2+ и3 + …+ иn+ … (1) σ1+ σ2+ σ3 + …+ σn+ …, (2)
причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. иn≤ σn (n = 1, 2, 3, …). Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).
Второй признак сравнения. Если существует конечный и отличный от нуля предел Признак Коши. Если для ряда (1) существует
Поиск по сайту: |











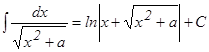
 б)
б)  в)
в) 
 .
.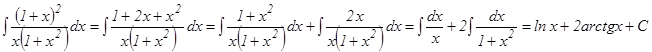
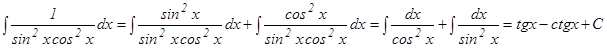
 не является табличным и не может быть найден способом непосредственно интегрирования, то введение новой переменной интегрирования позволяет свести данный интеграл к табличному. В этом сущность так называемого метода подстановки.
не является табличным и не может быть найден способом непосредственно интегрирования, то введение новой переменной интегрирования позволяет свести данный интеграл к табличному. В этом сущность так называемого метода подстановки. б)
б)  в)
в)  .
. . Производя замену, получаем:
. Производя замену, получаем: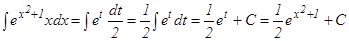
 ; следовательно,
; следовательно, .
.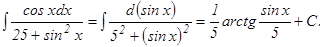
 – дифференцируемые функции от переменной х. Определим дифференциал произведения этих функций:
– дифференцируемые функции от переменной х. Определим дифференциал произведения этих функций: (1)
(1) есть более простой интеграл по отношению к данному интегралу
есть более простой интеграл по отношению к данному интегралу 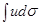 .
.
 .
.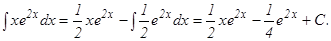

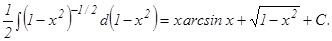
 , где Р(х) и Q(х) – многочлены. Рациональная дробь называется правильной, если степень многочлена Р(х) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.
, где Р(х) и Q(х) – многочлены. Рациональная дробь называется правильной, если степень многочлена Р(х) ниже степени многочлена Q(x); в противном случае дробь называется неправильной. II.
II.  , где m – целое число, m > 1;
, где m – целое число, m > 1;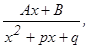 где
где  , т.е. квадратный трехчлен х2 + рх + q не имеет действительных корней;
, т.е. квадратный трехчлен х2 + рх + q не имеет действительных корней; где n – целое число, n > 1; т.е. квадратный трехчлен х2 + рх + q не имеет действительных корней.
где n – целое число, n > 1; т.е. квадратный трехчлен х2 + рх + q не имеет действительных корней. .
. .
. (здесь в знаменателе исходного интеграла выделили полный квадрат и свели к табличному интегралу).
(здесь в знаменателе исходного интеграла выделили полный квадрат и свели к табличному интегралу). - сводится к табличному либо путем различных преобразований подинтегральной функции, либо используя рекуррентную формулу.
- сводится к табличному либо путем различных преобразований подинтегральной функции, либо используя рекуррентную формулу.
 а множителю (х + 3) – простейшая дробь
а множителю (х + 3) – простейшая дробь  Итак, имеем:
Итак, имеем: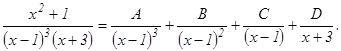

 .
.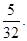
 т.е.
т.е. 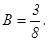
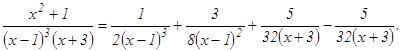
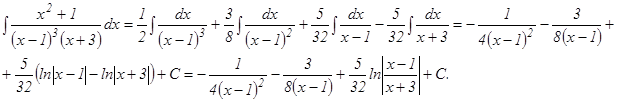

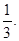

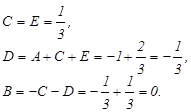
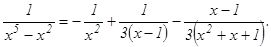
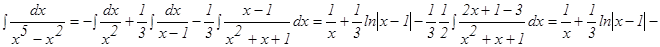
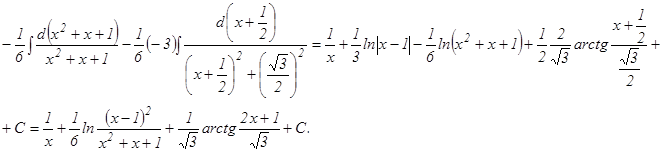
 Освобождаясь от знаменателя, получаем:х3- 2х = Ах + В + (Сх + D) (х2+ 1). Приравниваем коэффициенты при одинаковых степенях х:
Освобождаясь от знаменателя, получаем:х3- 2х = Ах + В + (Сх + D) (х2+ 1). Приравниваем коэффициенты при одинаковых степенях х: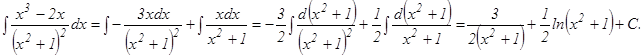

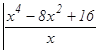
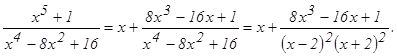
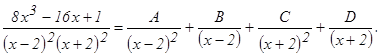
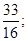

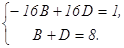
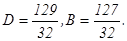

 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.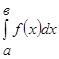 находят приближенно, например, применяя формулу Симпсона:
находят приближенно, например, применяя формулу Симпсона: (2)
(2)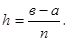
 .
. :
:
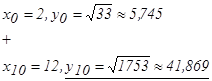
 47,614
47,614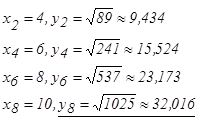
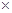

 (3)
(3) (4)
(4)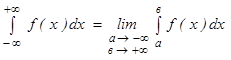 (5)
(5) (6)
(6) , где f(c) = ∞, a < c < в, называется сходящимся, если существуют оба предела в правой части равенства (6), и расходящимся, если не существует хотя бы один из них.
, где f(c) = ∞, a < c < в, называется сходящимся, если существуют оба предела в правой части равенства (6), и расходящимся, если не существует хотя бы один из них. б)
б)  в)
в) 
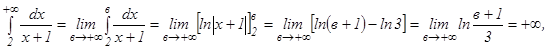
 следовательно, данный интеграл сходится и он равен
следовательно, данный интеграл сходится и он равен  .
.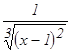 имеет бесконечный предел при х = 1, т.е. в точке, принадлежащей интервалу интегрирования.
имеет бесконечный предел при х = 1, т.е. в точке, принадлежащей интервалу интегрирования.
 и прямой у = х + 1.
и прямой у = х + 1.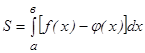 (7)
(7)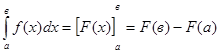 , (8)
, (8)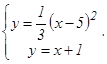
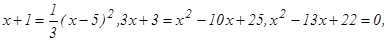
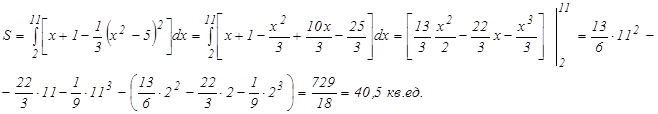
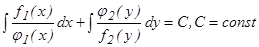
 (4)
(4)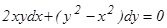

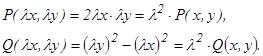
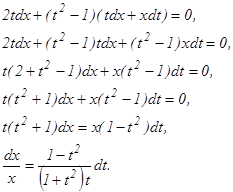
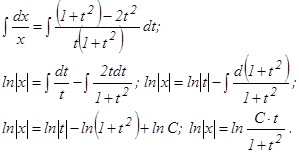
 или х (1 + t2) = Сt. Из введенной подстановки следует, что
или х (1 + t2) = Сt. Из введенной подстановки следует, что  Следовательно,
Следовательно,  или х2 + у2= Су – общее решение данного уравнения.
или х2 + у2= Су – общее решение данного уравнения.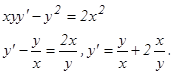
 , откуда
, откуда  где
где  Тогда последнее уравнение примет вид:
Тогда последнее уравнение примет вид: 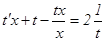 или
или 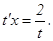
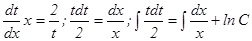
 или
или 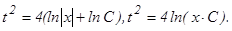
 или
или  - искомое общее решение ДУ.
- искомое общее решение ДУ.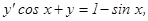

 (1)
(1) или
или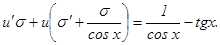
 (2)
(2) (3)
(3)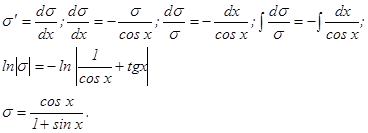
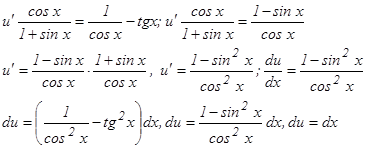

 или
или - общее решение уравнения (1).
- общее решение уравнения (1). , тогда
, тогда  и уравнение примет вид:
и уравнение примет вид: или
или (4)
(4) (6)
(6)
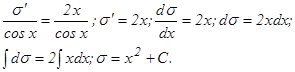
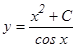 - общее решение данного уравнения.
- общее решение данного уравнения. (1)
(1) или
или (2)
(2) откуда z = xt, z΄=t΄x + t и уравнение примет вид:
откуда z = xt, z΄=t΄x + t и уравнение примет вид: или
или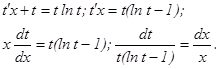
 , или
, или 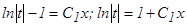
 или
или  откуда
откуда 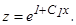
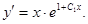
 Для нахождения данного интеграла применяем формулу интегрирования по частям:
Для нахождения данного интеграла применяем формулу интегрирования по частям: (3)
(3) dx, тогда du = dx,
dx, тогда du = dx,  Применяя формулу (3), получаем общее решение уравнения (1):
Применяя формулу (3), получаем общее решение уравнения (1):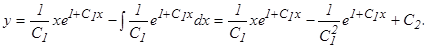
 … через z и производные от z по y, причем порядок уравнения понизится на единицу.
… через z и производные от z по y, причем порядок уравнения понизится на единицу. и данное уравнение примет вид:
и данное уравнение примет вид:  или
или  ; это уравнение первого порядка относительно z c разделяющимися переменными. Разделяем переменные и интегрируем:
; это уравнение первого порядка относительно z c разделяющимися переменными. Разделяем переменные и интегрируем: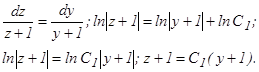
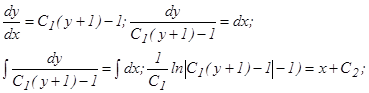
 – общий интеграл данного уравнения.
– общий интеграл данного уравнения. , (1)
, (1) и любого частного решения уч.н. данного неоднородного уравнения (1).
и любого частного решения уч.н. данного неоднородного уравнения (1). .
. .
. .
. , удовлетворяющее начальным условиям у(0)=у0, у′(0)=у′0.
, удовлетворяющее начальным условиям у(0)=у0, у′(0)=у′0.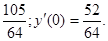
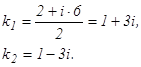
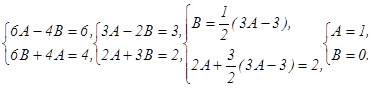
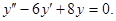
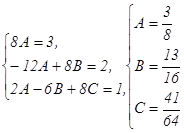
 или
или (24х2+52х+41).
(24х2+52х+41). ) получим
) получим =
=  ) получим второе уравнение с неизвестными С1 и С2.
) получим второе уравнение с неизвестными С1 и С2. =
= 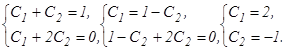
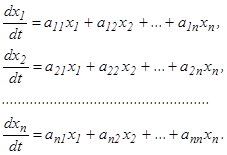
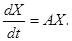
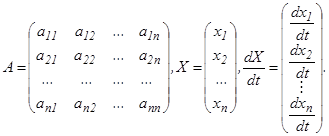
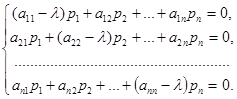
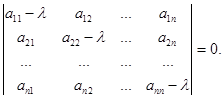
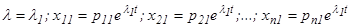
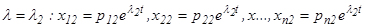
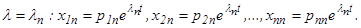
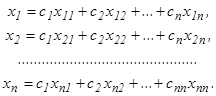

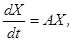
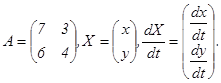
 или (7 – λ) (4 – λ) - 18 = 0, λ2- 11λ+ 10 = 0.
или (7 – λ) (4 – λ) - 18 = 0, λ2- 11λ+ 10 = 0. и сводится к одному уравнению 2р1+р2= 0. последнее определяет вектор с координатами (1; -2).
и сводится к одному уравнению 2р1+р2= 0. последнее определяет вектор с координатами (1; -2). или р1 – р2= 0. Это уравнение определяет вектор с координатами (1; 1). Получаем фундаментальную систему решения:
или р1 – р2= 0. Это уравнение определяет вектор с координатами (1; 1). Получаем фундаментальную систему решения: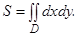
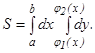

 . Из того, что в правой части равенства стоит двойной знак «±», а также из того, что ρ(-θ)=±а
. Из того, что в правой части равенства стоит двойной знак «±», а также из того, что ρ(-θ)=±а  :
:



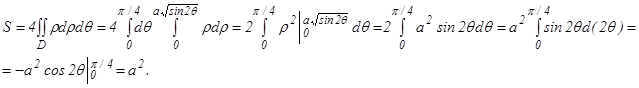
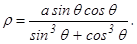


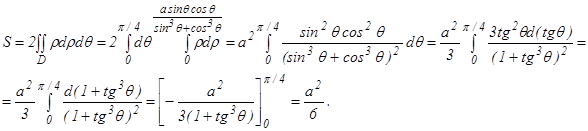
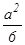 кв.ед.
кв.ед.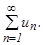
 т.е. при n→∞ предел общего члена сходящегося ряда равен нулю. Таким образом, если
т.е. при n→∞ предел общего члена сходящегося ряда равен нулю. Таким образом, если  то ряд расходится.
то ряд расходится. то оба ряда
то оба ряда  и
и  одновременно сходятся или одновременно расходятся.
одновременно сходятся или одновременно расходятся.