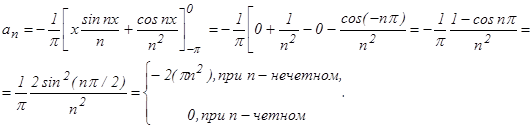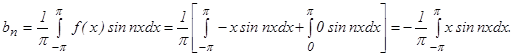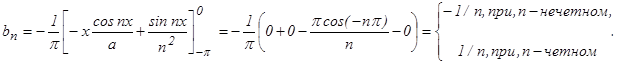 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Функциональные и степенные ряды
Пример 2. Найти область сходимости степенного ряда: Решение а) Данный степенной ряд можно записать так:
Применяем признак Даламбера и ищем предел:
Как видно, ряд будет сходиться для тех значений х, для которых Таким образом, интервал сходимости данного ряда (-2; 2). Граничные точки интервала сходимости х = При х = -2, получим числовой знакочередующийся ряд Следовательно, областью сходимости данного ряда является полуоткрытый интервал:
-2 ≤ х < 2
б) Здесь
Следовательно, заданный степенной ряд расходится при всех значениях х ≠ 0 и сходится только при х = 0.
Пример 3. Вычислить интеграл Решение Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд функции sin x, имеем:
Получен знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в этом ряде четвертый член по абсолютному значению меньше 0,001, то ограничимся только первыми тремя членами. Итак,
Пример 4. Найти первые три (отличные от нуля) члена разложения в ряд Маклорена функции у(х), являющейся частным решением дифференциального уравнения у΄ = х + х2-у2+ cos x, если у(0)=1.
Решение Положим, что у(х) является решением данного дифференциального уравнения при указанных начальных условиях. Если функцию у(х) можно разложить в ряд Маклорена, то
Свободный член разложения (1), т.е у(0), дан по условию. Чтобы найти значения у΄(0), у΄΄(0), у΄΄΄(0), …, можно данное уравнение последовательно дифференцировать по переменной х и затем вычислить значения производных при х=0. Значение у΄(0) получаем, подставив начальные условия в данное уравнение:
Подставив найденные значения производных при х=0 в (1), получим разложение искомого частного решения заданного уравнения:
Ряды Фурье
Пример 5. Разложить в ряд Фурье периодическую функцию f(x), заданную на интервале – периоде (π; π):
Решение. Заданная функция f(x) удовлетворяет условиям разложения в ряд Фурье, поэтому имеем равенство:
где an и bn определяются по формулам
Положив в (2) n = 0, получим коэффициент а0:
Используя формулу (2) и заданную функцию, имеем
Интегрируя по частям, получаем
Определим коэффициенты bn
Интегрируя по частям, получаем
Подставляя найденные значения коэффициентов Фурье в (1) получаем
Поиск по сайту: |
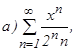
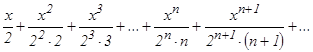
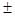2, для которых Д = 1 и признак Даламбера не решает вопроса о сходимости ряда, и исследуется особо.
для которого выполняются все условия признака Лейбница: 
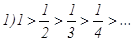и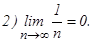 
Следовательно ряд сходится. При х = 2, получим гармоничный ряд 
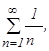который расходится.
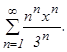Применим признак Коши, находя предел:
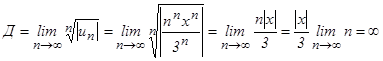при любом х ≠ 0.
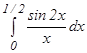с точностью до 0,001.
(1)
или
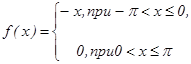
(1)
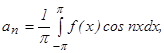n= 0, 1, 2, 3, … (2)
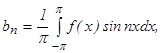n= 1, 2, 3, … (3)
