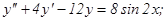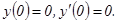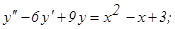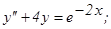|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Для студентов заочной формы обучения
Контрольная работа №1
1 - 10. Даны векторы а (а1; а2; а3), b (b1; b2; b3), с (с1; с2; с3) и d (d1; d2; d3) в некотором базисе. Показать, что векторы а, b, c образуют базис, и найти координаты вектора d в этом базисе.
1. а(1;2;3), b(-1;3;2), с(7;-3;5), d(6;10;17). 2. а(4;7;8), b(9;1;3), с(2;-4;1), d(1;-13;-13). 3. а(8;2;3), b(4;6;10), с(3;-2;1), d(7;4;11). 4. а(10;3;1), b(1;4;2), с(3;9;2), d(19;30;7). 5. а(2;4;1), b(1;3;6), с(5;3;1), d(24;20;6). 6. а(1;7;3), b(3;4;2), с(4;8;5), d(7;32;14). 7. а(1;-2;3), b(4;7;2), с(6;4;2), d(14;18;6). 8. а(1;4;3), b(6;8;5), с(3;1;4), d(21;18;33). 9. а(2;7;3), b(3;1;8), c(2;-7;4), d(16;14;27). 10. а (7;2;1), b(4;3;5), с(3;4;-2), d(2;-5;-13).
11 - 20. Даны координаты вершин пирамиды А1А2А3А4. Найти 1) длину ребра А1А2; 2) угол между ребром А1А2 и А1А4; 3) угол между ребрами А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
11. А1 (4;2;5), А2 (0;7;2), А3 (0;2;7), А4 (1;5;0). 12.А1 (4;4;10), А2 (4;10;2), А3 (2;8;4), А4 (9;6;4). 13.А1 (4;6;5), А2 (6;9;4), А3 (2;10;10), А4 (7;5;9). 14.А1 (3;5;4), А2 (8;7;4), А3 (5;10;4), А4 (4;7;8). 15.А1 (10;6;6), А2 (-2;8;2), А3 (6;8;9), А4 (7;10;3). 16.А1 (1;8;2), А2 (5;2;6), А3 (5;7;4), А4 (4;10;9). 17.А1 (6;6;5), А2 (4;9;5), А3 (4;6;11), А4 (6;9;3). 18.А1 (7;2;2), А2 (5;7;7), А3 (5;3;1), А4 (2;3;7). 19.А1 (8;6;4), А2 (10;5;5), А3 (5;6;8), А4 (8;10;7). 20.А1 (7;7;3), А2 (6;5;8), А3 (3;5;8), А4 (8;4;1).
21.Уравнение одной из сторон квадрата х + 3у – 5 = 0. Составить уравнения трех остальных сторон квадрата, если (-1;0) – точка пересечения его диагоналей.
22.Даны уравнения одной из сторон ромба х - 3у + 10 = 0 и одной из его диагоналей х + 4у – 4 = 0; диагонали ромба пересекаются в точке (0, 1). Найти уравнения остальных сторон ромба.
23.Уравнения двух сторон параллелограмма х + 2у + 2 = 0 и х + у = 0, а уравнение одной из его диагоналей х – 2 = 0. Найти координаты вершин параллелограмма.
24.Даны две вершины А(-3;3) и В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон.
25.Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВСD (AD
26.Даны уравнения двух сторон треугольника 5х - 4у + 15 = 0 и 4х + у – 9 = 0. Его медианы пересекаются в точке (0;2). Составить уравнение третьей стороны треугольника.
27.Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С.
28.Даны уравнения двух высот треугольника х + у = 4 и у = 2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника.
29.Даны уравнения двух медиан треугольника х - 2у + 1 = 0 и у – 1 = 0 и одна из его вершин (1;3). Составить уравнения его сторон.
30.Две стороны треугольника заданы уравнениями 5х - 2у – 8 = 0 и 3х - 2у – 8 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
31.Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки А(5;0) относятся как 2:1.
32.Составить уравнение линии, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее от прямой х = - 4.
33.Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 5х + 8 = 0 относятся как 5 : 4.
34.Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
35.Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 2х + 5 = 0 относятся как 4 : 5.
36.Составить уравнение линии, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В(26;0).
37.Составить уравнение линии, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у – 4 = 0.
38.Составить уравнение линии, каждая точка которой равноотстоит от оси ординат и от окружности х2 + у2 = 4х.
39.Составить уравнение линии, каждая точка которой равноудалена от точки А(2;6) и о прямой у + 2 = 0.
40.Составить уравнение линии, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.
41 – 50. Линия задана уравнением r = r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
41. 43. 45. 47. 49.
42. 44. 46. 48. 50.
51 - 60. Дана система линейных уравнений:
Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления. 51. 53. 55. 57. 59. 61 - 80. Решить систему трех уравнений с тремя неизвестными при помощи определителей.
61.
63.
65.
67.
69.
71.
73.
75.
77.
79. Контрольная работа №2 81 - 90. Дано комплексное число а. Требуется:1) записать число а в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3 + а = 0.
81. 83. 85. 87. 89.
91 - 95. Построить график функции у = Аsin(ax+b) преобразованием графика функции у = sin x. 91. 92. 93. 94. 95. 96 - 100. Построить график функции y = A cos(ax+b) преобразованием графика функции y = cos x. 96. 97. 98. 99. 100.
101 - 120. Найти пределы функций, не пользуясь правилом Лопиталя.
121 - 130. Задана функция y = f(x) и два значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж. 121. f(x)=91/(2-x), x1=0, x2=2. 123. f(x)=121/x, x1=0, x2=2. 125. f(x)=81/(5-x), x1=3, x2=5. 127. f(x)=141/(6-x), x1=4, x2=6. 129. f(x)=111/(4+x), x1=-4, x2=-2. 122. f(x)=41/(3-x), x1=1, x2=3. 124. f(x)=31/(4-x), x1=2, x2=4. 126. f(x)=101/(7-x), x1=5, x2=7. 128. f(x)=151/(8-x), x1=6, x2=8. 130. f(x)=131/(5+x), x1=-5, x2=-3.
В задачах 131 - 140 даны функции y = f(x) и значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3)построить график данной функции.
131. 133. 135. 137. 139. 132. 134 136. 138. 140. В задачах 141 - 150 функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) сделать чертеж.
151 - 160. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
151. 152. 153. 154. 155. 156. 157. 158. 159. 160.
Контрольная работа №3 161 - 170. Найти производные
171 - 180. Найти 171. 172. 173. 174. 175. 176. 177. 178. 179. 180.
181 - 190. Найти наибольшее и наименьшее значения функции у = f(x) на отрезке 181. 182. 183. 184. 185. 186. 187. 188. 189. 190. 191 - 210. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191. у = 4х/(4+х2) 192. y = (x2-1)/(x2 +1) 193. y = (x2+1)/(x2-1) 194. y = x2/(x-1) 195. y = x3/(x2+1) 196. y = (4x3+5)/x 197. y = (x2-5)/(x-3) 198. y = x4/(x3-1) 199.y = 4x3/(x3-1) 200. y = (2-4x2)/(1-4x2) 201. y = (1nx)/ 203. y = 205. y = 1n (x2-4) 206. y = e1/(2-x) 207. y = 1n (x2+1) 208. y = (2+x2) 209. y = 1n (9-x2) 210. y = (x-1)e3x+1.
211. Дана функция z = y/(x2- y2)5. Показать, что 212. Дана функция z = y2/(3x)+arcsin(xy). Показать, что 213. Дана функция z = 1n(x2+y2+2x+1). Показать, что 214. Дана функция z = exy. Показать, что 215. Дана функция z = 1n(x+e-y). Показать, что 216. Дана функция z = x/y. Показать, что 217. Дана функция z = xy. Показать, что 218. Дана функция z = xey/x. Показать, что 219. Дана функция z = sin(x+ay). Показать, что 220. Дана функция z = cosy+(y - x)siny. Показать, что
221 - 230. Дана функция z = f(x,y) и две точки А(х0, у0) и В(х1, у1). Требуется: вычислить значение z1 функции в точке В; 2) вычислить приближенное значение
221. z = x2+xy+y2; А(1;2), В(1,02;96) 222. z = 3x2-xy+x+y; А(1;3), В(1,06;2,92) 223. z = x2+3xy-6y; А(4;1), В(3,96;1,03) 224. z = x2-y2+6x+3y; А(2;3), В(2,02;2,97) 225. z = x2+2xy+3y2 ; А(2;1), В(1,96;1,04) 226. z = x2+y2+2x+y-1; А(2;4), В(1,98;3,91) 227. z = 3x2+2y2-xy; А(-1;3), В(-0,98;2,97) 228. z = x2-y2+5x+4y; А(3;3), В(3,02;2,98) 229. z = 2xy+3y2-5x; А(3;4), В(3,04;3,95) 230. z = xy+2y2-2x; А(1;2), В(0,97;2,03).
231 - 240. Найти наименьшее и наибольшее значения функции z = f(x,y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
231. z = x2+y2-9xy+27; 232. z = x2+2y2+1; 233. z = 3-2x2-xy-y2; 234. z = x2+3y2+x-y; 235. z = x2+2xy+2y2; 236. z = 5x2-3xy+y2+4; 237. z = 10+2xy-x2; 238. z = x2+2xy-y2+4x; 239. z = x2+xy-2; 240. z = x2+xy;
241 - 250. Даны функции z = z(x,y), точка А(х0,у0) и вектор а. Найти; 1) grad z в точке А; 2)производную в точке А по направлению вектора а.
241. z = x2+xy+y2; А(1;1), а = 2i-j. 242. z = 2x2+3xy+y2; А(2;1), a = 3i-4j. 243. z = 1n(5x2+3y2); А(1;1), a = 3i+2j. 244. z = 1n(5x2+4y2); А(1;1), a = 2i-j. 245. z = 5x2+6xy; А(2;1), a = i+2j. 246. z = arctg(xy2); А(2;3), a = 4i-3j. 247. z = arcsin (x2/y); А(1;2), a = 5i-12j. 248. z = 1n(3x2+4y2); А(1;3), a = 2i-j. 249. z = 3x4+2x2y3; А(-1;2), a = 4i-3j. 250. z = 3x2y2+5y2x; А(1;1), a = 2i+j.
251 - 260. Экспериментально получены пять значений искомой функции y = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f(x) в виде у = ах + b. 251.
252.
253.
254.
255.
256.
257.
258.
259.
260.
Контрольная работа №4 261 - 270. Найти неопределенные интегралы. В двух первых примерах а) и б) проверить результаты дифференцированием.
261. 262. 263. 264. 265. 266. 267. 268. 269. 270.
271 - 280. Вычислить приближенное значение определенного интеграла 271. 273. 272. 274. 275. 277. 279. 276. 278. 280.
281 - 290. Вычислить несобственный интеграл или доказать его расходимость. 281. 283. 285. 287. 289. 282. 284. 286. 288. 290. 291. Вычислить площадь фигуры, ограниченной параболой у = 3х2 + 1 и прямой у = 3х + 7. 292. Вычислить площадь фигуры, ограниченной одной аркой циклоды х = а(t - sin t), y = a(1 - cos t),
293. Вычислить площадь фигуры, ограниченной кардиоидой r = 3(1 + cos φ).
294. Вычислить площадь фигуры, ограниченной четырехлепестковой розой r = 4sin 2φ. 295. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами у = х2 и у =
296. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом у =
297. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2/(1 + х2)4 и у = х2.
298. Вычислить длину дуги полукубической параболы у =
299. Вычислить длину кардиоиды r = 3(1 - cosφ).
300. Вычислить длину одной арки циклоиды х = 3(t - sint), y = 3(1 - cost), 301 - 320. Найти общее решение дифференциального уравнения.
301. 302. 303. 304. 305. 306. 307. 308. 309. 310. 311. 312. 313. 314. 315. 316. 317. 318. 319. 320. В задачах 321 - 330 даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
321. у΄΄- еуу΄= 0, у(0) = 0, у΄(0) = 1. 322. у΄у΄΄= 2у, у(0) = 0, у΄(0) = 0. 323. уу΄΄= (у΄)2, у(0) = 1, у΄(0) = 3. 324. у3у΄΄= 3, у(1) = 1, у΄(1) = 1. 325. у΄΄-12у2= 0, у(0) =1/2, у΄(0) = 1. 326. 2у΄΄=е4у, у(0) = 0, у΄(0) = ½. 327. (у – 2)у΄΄ = 2(у΄)2, у(0) = 3, у΄(0) = 1. 328. 2уу΄΄= 3 + (у΄)2, у(1) = 1, у΄(1) = 1. 329. у΄΄= 330. (у + 1)2у΄΄= (у΄)3, у΄(0) = 1. 331 - 340. Найти частное решение дифференциального уравнения 331. 332. 333.
Поиск по сайту: |
 ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
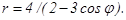
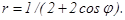
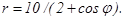
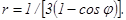
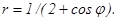

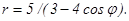
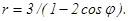
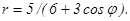
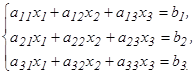
 52.
52. 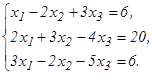
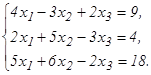 54.
54. 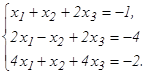
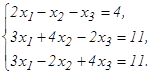 56.
56. 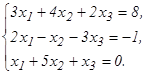
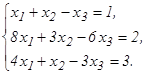 58.
58. 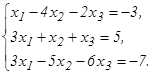
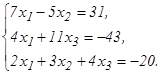 60.
60. 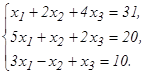
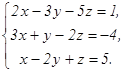 62.
62. 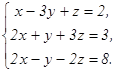
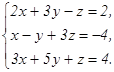 64.
64. 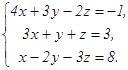
 66.
66. 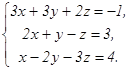
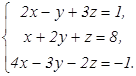 68.
68. 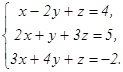
 70.
70. 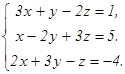
 72.
72. 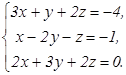
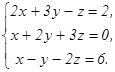 74.
74. 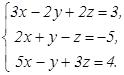
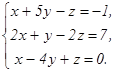 76.
76. 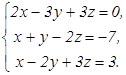
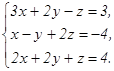 78.
78. 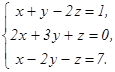
 80.
80. 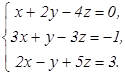
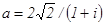 . 82.
. 82. 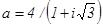 .
.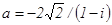 . 84.
. 84. 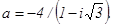
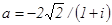 . 86.
. 86. 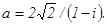
 . 88.
. 88.  .
.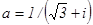 . 90.
. 90. 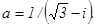 .
. .
.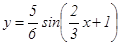 .
.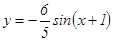 .
.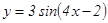 .
.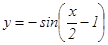 .
.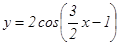 .
.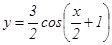 .
.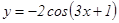 .
.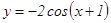 .
. .
.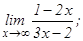


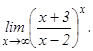
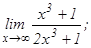
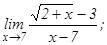
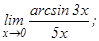

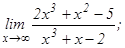
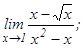
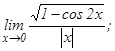
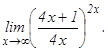

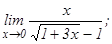

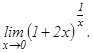
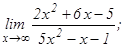
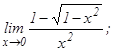

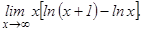

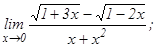
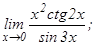
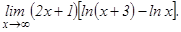
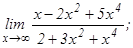
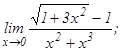
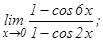

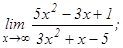

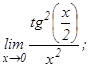
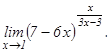

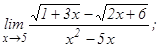
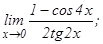
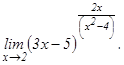

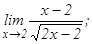

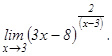
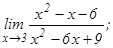
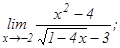

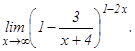
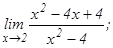
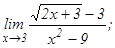
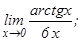

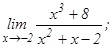
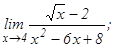
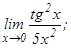

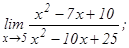
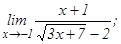


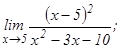


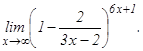
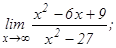
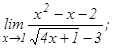


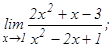
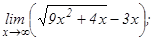

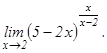


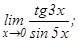

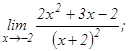
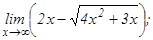
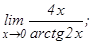
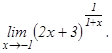



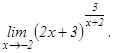

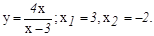
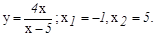
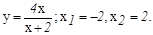


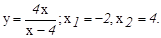


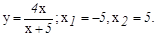
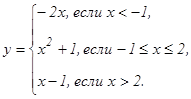
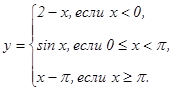
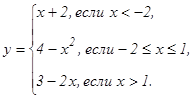


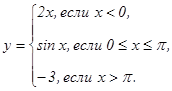
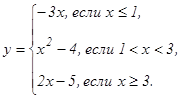

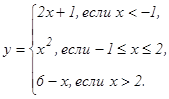
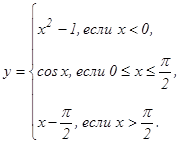
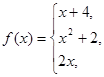

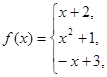
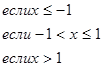


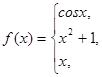
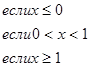

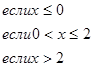
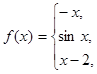

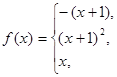
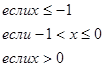
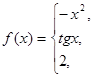


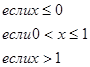
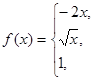
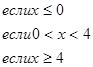
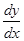 данных функций.
данных функций.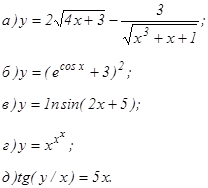


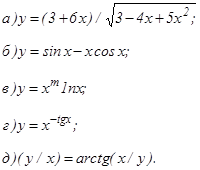


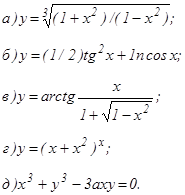
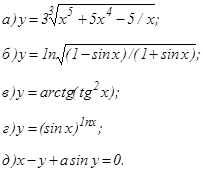


 и
и 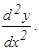
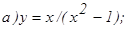

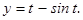



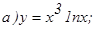


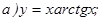
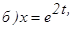
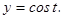
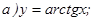

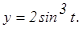
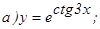

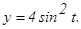

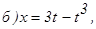


 ,
, 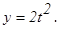
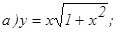
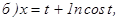
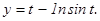
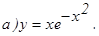

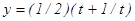 .
.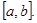
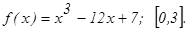




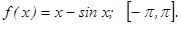
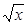 202. y = x
202. y = x 
 204. y = x2-21nx
204. y = x2-21nx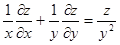
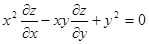
 функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С(х0, у0, z0).
функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С(х0, у0, z0).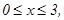
 .
.
 .
.
 .
.

 .
.
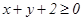 .
.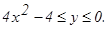

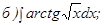
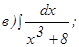

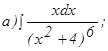

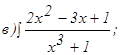
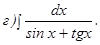
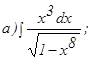
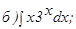

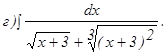
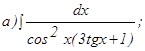
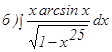 ;
;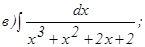
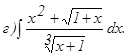
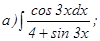
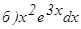 ;
;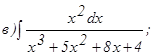
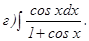

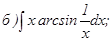


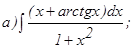
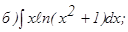
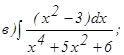
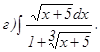

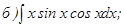

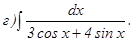
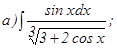

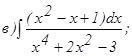


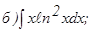
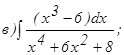
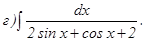
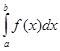 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
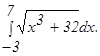
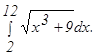

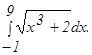
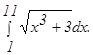



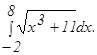




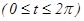 и осью Ох.
и осью Ох. .
. , параболой х =
, параболой х =  и осью Оу.
и осью Оу.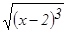 от точки А (2;0) до точки В (6;8).
от точки А (2;0) до точки В (6;8).

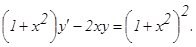
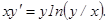


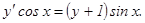
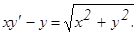
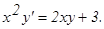
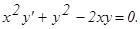
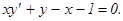
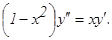
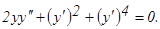
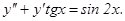

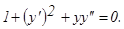
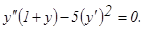
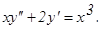


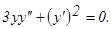
 у(2) = 0, у΄(2) = 2.
у(2) = 0, у΄(2) = 2.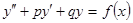 , удовлетворяющее начальным условиям у(0)=у0,
, удовлетворяющее начальным условиям у(0)=у0,