 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
I. Элементы линейной алгебры и аналитической геометрии
Пример 1. Даны векторы
Решение. Выражение х1+
то говорят, что вектор
имеет место только при нулевых значениях коэффициентов х1, х2, … , хк, если же равенство (2) выполняется и при условии, что хотя бы один из коэффициентов х1, х2, … , хк, отличен от нуля, то система векторов Для векторов с заданными координатами
Подставим в (3) данные векторы
Так как
Составим матрицу системы и преобразуем ее к треугольному виду, т.е. будем последовательно получать нули ниже главной диагонали матрицы, на которых находятся элементы 2, 2, 8, 3.
Разделим каждый элемент I строки на 2, затем полученную I строку умножим последовательно на -4; -3; -2 и сложим соответственно со II; III и IV строками, получим:
Разделим III строку на (-2) и поменяем ее местами со II строкой.
Новую II строку умножим последовательно на 3; -2 и сложим соответственно с III и IV строками, получим:
III строку умножим на 5, IV на 6 и сложим их, получим:
Таким образом получим матрицу ступенчатого вида, например х1, х2, х3, х4,
откуда х4 = 3, х3 = -1, х2 = 0, х1 = 2. Решение системы * (2; 0; -1; 3) образует совокупность координат вектора
Пример 2. Даны координаты вершин пирамиды А1(2; 1; 0), А2(3; -1; 2), А3(13; 3; 10), А4(0; 1; 4). Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребрами А1А4 и гранью А1 А2 А3; 4) площадь грани А1 А2 А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1 А2 А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3 . Сделать чертеж.
Решение. 1) Расстояние d между точками А(х1, y1, z1) и В(х2, y2, z2), определяется по формуле
Подставим в (1) координаты точек А1 и А2 , находим длину ребра А1А2:
А1А2= 2) Угол между ребрами А1А2 и А1А4 равен углу φ между направляющими векторами этих ребер
Координаты вектора
Применяя (3), получим
Скалярное произведение двух векторов с заданными координатами равны сумме произведений соответствующих координат, т.е если
Применяя (4), найдем
3) Угол между ребром А1А4 и гранью А1 А2 А3 равен углу φ между направляющим вектором Уравнение плоскости, проходящей через 3 данные точки А1(х1, y1, z1) и А2(х2, y2, z2), А3(х3, y3, z3) имеет вид
Подставим в (5) координаты точек А1 А2 А3, получим:
Разложим определитель по элементам I строки:
Сократив на (-12), получим уравнение плоскости А1 А2 А3 : 2x – 4 – y + 1 - 2z = 0 2x – y - 2z – 3 = 0 Если уравнение плоскости α задано в каноническом виде Ax + By + Cz + Д = 0, то ее нормальный вектор
Найдем скалярное произведение
Поиск по сайту: |
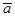 1(2 ; 4 ; 3 ; 2),
1(2 ; 4 ; 3 ; 2),  (18 ; 24 ; 13 ; 6). Показать, что векторы
(18 ; 24 ; 13 ; 6). Показать, что векторы  1,
1,  (1)
(1)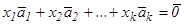 (2)
(2) (3)
(3)
 , то векторы линейно независимы и они образуют базис линейного пространства R4 . Для вычисления координат вектора
, то векторы линейно независимы и они образуют базис линейного пространства R4 . Для вычисления координат вектора  *
*
 ~
~ 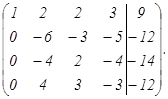
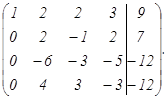
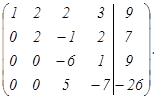

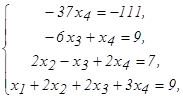
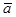 1 -
1 -  (1)
(1)
 и
и  . Косинус угла между двумя векторами = скалярному произведению этих векторов, деленному на произведение их модулей:
. Косинус угла между двумя векторами = скалярному произведению этих векторов, деленному на произведение их модулей: (2)
(2)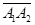 с началом в точке А1(x1, y1, z1) и концом в точке А2(x2, y2, z2)
с началом в точке А1(x1, y1, z1) и концом в точке А2(x2, y2, z2) (3)
(3) (-2; 0; 4). Применяя (1), получим модули векторов
(-2; 0; 4). Применяя (1), получим модули векторов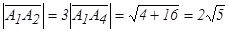
 ), то их скалярное произведение
), то их скалярное произведение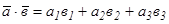 (4)
(4) . Следовательно,
. Следовательно,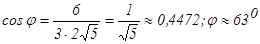
 плоскости А1 А2 А3 .
плоскости А1 А2 А3 . (5)
(5)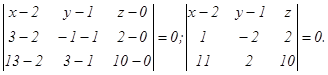
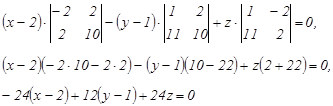
 (6)
(6)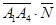 по формуле (4):
по формуле (4): = -2 2 + 0 (-1) + 4 (-2) = - 4 – 8 = -12.
= -2 2 + 0 (-1) + 4 (-2) = - 4 – 8 = -12.