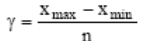|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интервал дискретизации
Пусть известна кривая x(t). Если вследствие погрешностей и помех достоверными являются только значения, разделенные промежутками Δx, то проецируя эти точки на ось времени получим промежутки τi, через которые целесообразно производить отсчеты (рис.2 Таким образом, дискретность по оси t полностью определяется квантованием по уровню и крутизной функции x(t). Функцию x(t) можно аппроксимировать ломаной линией. Тогда
В предельных случаях: а) при установившемся значении (dx/dt)→ 0, τi→∞ ; б) при скачке (dx/dt)→ ∞, τi→0 . Теоретическое обоснование процесса дискретизации информации содержит теорема Котельникова. Она использует представление сигнала в виде спектра гармоник. Реальный измеряемый сигнал всегда наблюдается в условиях помех, т.е. представляет собой реализацию случайного процесса. В некоторых случаях влиянием случайной компоненты (шума) можно пренебречь и считать сигнал квазидетерминированным. Для анализа сложный квазидетерминированный сигнал удобно разложить на сумму элементарных функций ϕk(t), обладающих известными свойствами
где Ak – коэффициент разложения, называемый спектром. Обычно для разложения используют систему функций, отвечающих на некотором интервале времени (tn,tk ) условию ортогональности
Система функций ϕk(t) называется ортонормированной, если она удовлетворяет также условию Система ортогональных функций, используемых для разложения сложного квазидетерминированного сигнала в ряд, называется обобщенным рядом Фурье, а соответствующие коэффициенты разложения – обобщенным спектром Фурье. Наиболее часто используется разложение сигнала x(t) в ряд по системе тригонометрических функций. Для периодического сигнала с периодом T это разложение имеет вид:
где Ak,φk - амплитуда и начальная фаза k-й гармоники.
Теорема о дискретизации сигнала, известная как теорема Котельникова, так определяет правило дискретизации: всякий непрерывный сигнал x(t), обладающий ограниченным спектром частот, не содержащим частот выше, чем Fгр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга во времени на интервалы
и может быть восстановлен по формуле
где F0 – частота дискретизации. Из теоремы Котельникова следует, что частота дискретизации должна отвечать условию F0 ≥ 2Fгр (условие Найквиста), в противном случае возникает эффект наложения или подмены частот, который является причиной погрешности при восстановлении сигнала. Теорема Котельникова предполагает ограниченный спектр частот и бесконечную протяженность во времени (надо знать все прошлые и будущие значения), тогда как реальный сигнал имеет конечную длительность и неограниченный частотный спектр. В этом случае применение теоремы Котельникова дает несколько завышенную частоту F0. На практике частоту преобразования устанавливают по соотношению F0 = k·2fm , (2) где fm – принятая максимальная частота в спектре сигнала, а k – коэффициент запаса, обычно 1,5 ≤ k ≤ 6 . (Для случайных процессов с ограниченным спектром период дискретизации входного сигнала по времени выбирается согласно теореме Котельникова. Квантование по уровню Квантование по уровню представляет собой преобразование множества значений сигнала x(ti) в дискретное множество значений xk
При неравномерном квантовании шаг квантования γk=xk-xk-1 между соседними уровнями xk и xk-1 изменяется. При выбранном шаге квантования могут быть следующие способы отнесения значений x(ti) сигнала к соответствующему уровню квантования: а) сигнал отождествляется с ближайшим уровнем квантования; б) сигнал отождествляется с меньшим уровнем квантования; в) сигнал отождествляется с большим уровнем квантования.
В случае а) максимальная погрешность квантования не превышает 0,5γk, а в случаях б), в) погрешность может быть в два раза больше - γk. Если рассматривать сигнал x(ti) как реализацию случайной величины X с плотностью распределения вероятности p(x) и принять, что шаг квантования γk мал по сравнению с диапазоном изменения сигнала, то для погрешности квантования Δxk=x-xk будет справедливо: математическое ожидание M[Δxk]=0; дисперсия
где p(xk) – вероятность попадания величины x в интервал γk.
Поиск по сайту: |
 Выбор интервала дискретизации).
Выбор интервала дискретизации). где tgαi= (dx/dt)i – скорость изменения функции на участке i, т.е.
где tgαi= (dx/dt)i – скорость изменения функции на участке i, т.е.

 при k≠n (k,n = 1,2,...N).
при k≠n (k,n = 1,2,...N).


 (1)
(1) , где
, где  - верхняя частота спектра сигналов. Для детерминированных процессов (закон изменения известен) этот интервал выбирается исходя из условия непревышения входной величины порога квантования по уровню.)
- верхняя частота спектра сигналов. Для детерминированных процессов (закон изменения известен) этот интервал выбирается исходя из условия непревышения входной величины порога квантования по уровню.)  [xmin,xmax], где k=1,2,...,n. Эти значения называются уровнями квантования. Квантование тоже может быть равномерным и неравномерным. При равномерном квантовании весь диапазон сигнала x(t) разбивается на n уровней с шагом квантования
[xmin,xmax], где k=1,2,...,n. Эти значения называются уровнями квантования. Квантование тоже может быть равномерным и неравномерным. При равномерном квантовании весь диапазон сигнала x(t) разбивается на n уровней с шагом квантования