 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коректуючі коди Хеммінга. Колєнов С.О
Спочатку про основні характеристики коректуючих кодів: 1) Число дозволених і заборонених комбінацій. Якщо
2) Надлишковість
3) Мінімальна кодова відстань. Дозволена комбінація повинна максимально відрізнятись від забороненої. Приклад: є дві послідовності:
Щоб знайти мінімальну кодову відстань між кодами Чим більше d, тим стійкіша система до помилок. Коди Хеммінга – відносяться до класу системних кодів, для яких характерно те, що будь-яка дозволена кодова комбінація може бути отримана в результаті лінійних операцій над набором незалежних лінійних кодових комбінацій. Коди Хеммінга відносяться до самоконтролюючих і самокоректуючих кодів, тут можливе автоматичне виправлення помилок. Побудовані вони відносно двійкової системи числення. Іншими словами, це алгоритм, який дозволяє закодувати будь інформаційне повідомлення певним чином і після передачі (наприклад по мережі) визначити, чи з'явилася якась помилка в цьому повідомленні (наприклад через перешкоди) і, при можливості, відновити це повідомлення. Найпростіший алгоритм Хеммінга може виправляти лише одну помилку. Також варто зазначити, що існують більш досконалі модифікації даного алгоритму, які дозволяють виявляти (і якщо можливо виправляти) більшу кількість помилок. Код Хеммінга складається з двох частин. Перша частина кодує вихідне повідомлення, вставляючи в нього в певних місцях контрольні біти (обчислені особливим чином). Друга частина отримує вхідне повідомлення і заново обчислює контрольні біти (за тим же алгоритмом, що і перша частина). Якщо всі знову обчислені контрольні біти збігаються з отриманими, то повідомлення отримано без помилок. В іншому випадку, виводиться повідомлення про помилку і при можливості помилка виправляється. Побудова коду Хеммінга базується на перевірці ваги слова на парність. Правило формування перевірочного символу
Критерій правильності комбінації – синдром:
Записується такий код Хеммінга як коректуючий код (n, n-1) або (k+1,k) – в цих дужках перше число відповідає загальній кількості бітів в повідомленні, а друге – число інформаційних бітів. Для коду Хеммінга повинно бути Класичний код Хеммінга: (n, k) = (2r-1,2r-1-r), де r – загальна кількість перевірочних символів. Повними кодами Хеммінга називають ті, для яких: (7,4), (15,11), (31,26) і т.д. Якщо k – менше, ніж зазначено в повних кодах Хеммінга, то такі коди називаються усіченими, наприклад код (9,5). Приклад для коду (7,4).
Перевіряючих біти 7-4=3:
Зазвичай ці перевіряючи біти розташовують в місцях, що відповідають степеням двійки: три перевірочних біти
В декодері на приймальній стороні сформовано три окремих біти – синдроми, які будуть перевіряти правильність отриманих комбінацій за рахунок того, що разом з інформаційними бітами будуть передаватись перевіряючи коди. Синдром:
Синдром характеризує конфігурацію помилок. Кількість можливих синдромів Якщо значення синдрому дорівнює нуль – то помилки немає, якщо 1 – то є.
Якщо в синдромі S лише одна одиниця , то помилка в перевірочному біті, в тому, на місці якого помилка, наприклад в таблиці, в першому стовпці, помилка в третьому перевірочному біті, бо одиниця в синдромі знаходиться на місці Розширений код Хеммінга, в якому вводиться додатковий біт, наприклад (7,4) -> (8,4), дозволяє виявити дві помилки в повідомленні. Додається ще один перевірочний біт:
Виникає необхідність ввести ще один біт синдрому
Якщо !!!!!! Необов’язково писати далі!!!!!! Якщо певний код Хеммінга складається з векторів
Коефіцієнти bij є елементами кінцевого поля F. З них можна зробити перевіряючу матрицю Н, вона дає всі можливі вектори синдромів. Для коду Хеммінга (7,4) перевіряюча матриця:
Всі рядки такої матриці лінійно незалежні. Існує ще так звана породжуючи матриця, вона дає базисні вектори можливих кодів Хеммінга, але вона визначається неоднозначно, оскільки базис можна задати довільним чином, тому наводити її тут не будемо. Її легко отримати з перевірочної матриці, наклавши деяку умову на необхідні вектори кодів Хеммінга.
Поиск по сайту: |
 - число всіх можливих комбінацій кодів,
- число всіх можливих комбінацій кодів,  - число дозволених комбінацій, то число заборонених комбінацій:
- число дозволених комбінацій, то число заборонених комбінацій:  .
. ,
,  - число перевірочних розрядів.
- число перевірочних розрядів. . Частину, яку в повному коді займає, інформаційне повідомлення, обчислюють, як:
. Частину, яку в повному коді займає, інформаційне повідомлення, обчислюють, як:
 . Вага комбінації W=3 (кількість одиниць в коді).
. Вага комбінації W=3 (кількість одиниць в коді). . Вага комбінації W=2
. Вага комбінації W=2 і
і  , треба просумувати їх за модулем 2. Отримаємо
, треба просумувати їх за модулем 2. Отримаємо  і мінімальна кодова відстань це вага цієї комбінації: d=3.
і мінімальна кодова відстань це вага цієї комбінації: d=3. :
:
 - складання по модулю 2,
- складання по модулю 2, 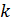 - загальна кількість інформаційних бітів.
- загальна кількість інформаційних бітів.
 , якщо
, якщо  , то корекцію коду зробити неможливо, можна тільки виявити помилки в ньому.
, то корекцію коду зробити неможливо, можна тільки виявити помилки в ньому.




 ,
, 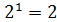 ,
,  . Тому вирази для перевіряючих бітів саме такі.
. Тому вирази для перевіряючих бітів саме такі.



 .
.
 . Якщо в синдромі більше однієї одиниці, то треба дивитись по першій таблиці, той інформаційний біт, що є в обох перевірочних бітах, на місці яких в синдромі – одиниці, - є помилковим.
. Якщо в синдромі більше однієї одиниці, то треба дивитись по першій таблиці, той інформаційний біт, що є в обох перевірочних бітах, на місці яких в синдромі – одиниці, - є помилковим.

 , то це вказує на поодиноку помилку, яку можна визначити за попередніми бітами синдрому, якщо помилки дві, то
, то це вказує на поодиноку помилку, яку можна визначити за попередніми бітами синдрому, якщо помилки дві, то  , а попередні біти синдрому при цьому повинні не дорівнювати нулю.
, а попередні біти синдрому при цьому повинні не дорівнювати нулю. і координати векторів є елементами кінцевого поля F, то ці вектори будуть задовольняти перевіряючим співвідношенням
і координати векторів є елементами кінцевого поля F, то ці вектори будуть задовольняти перевіряючим співвідношенням
