 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Хвильове рівняння поширення поверхневих акустичних хвиль Релея. Граничні умови для акустичних хвиль. Нечипорук О. Ю
Хвильове рівняння описує процес поширення пружних хвиль в твердому тілі. Спочатку виведемо хвильове рівняння без врахування п’єзоефекту. Основні рівняння, які будуть використаними: · закон Гука · другий закон динаміки (другий закон Ньютона) В ізотропному середовищі закон Гука виглядає так: де Тобто, ми зробили відповідні заміни: Другий закон Ньютона в тензорномувигляді є таким: Підставимо вигляд рішення в хвильове рівняння та маємо: Тепер врахуємо п’єзоефект в рівнянні для акустичних хвиль. Це можна зробити якщо врахувати п’єзоелектричний тензор еkij який пов’язує пружні напруження з електричними полями в п’єзоелектричному кристалі. При аналізі поширення пружних хвиль в п’єзоелектриках необхідно одночасно розв’язувати систему рівнянь з: - закону Гука ; - другого закону Ньютона; - системи рівнянь Максвела. Її розв’язком можуть буди два типи хвиль: - пружно-електромагнітні хвилі – це будуть переважно пружні хвилі із швидкістю поширення, яка дорівнює фазовій швидкісті АХ V (з рівняння Гріна-Кристофеля); ці хвилі будуть супроводжуватися наявним електричним полем - електромагнітно-пружні хвилі – це будуть переважно електромагнітні хвилі із швидкістю поширення, близькій до швидкості світла; ці хвилі будуть супроводжуватися механічною деформацією середовища їх поширення. І. Пружно-електромагнітні хвилі. Нехтуємо магнітною складовою електромагнітного поля, що створюється електричним полем в п’єзоелектрику та використовуємо рівняння Максвела в наближенні електростатики:
ІІ. Електромагнітно-пружні хвилі. Для цих коливань характерним є малість пружної складової енергії у порівнянні з електромагнітною. В цьому випадку не можна робити спрощень, а треба взяти повну систему рівнянь (закону Гука (1), другого закону Ньютона (2) та рівняння п’єзоефекту (3)) і її розв’язувати. Запишемо цю систему: Розв’язок цієї системи шукаємо у вигляді плоских хвиль:
Поиск по сайту: |
 , де Е – це модуль Юнга,
, де Е – це модуль Юнга,  - відносне видовження,
- відносне видовження,  - напруження (але такий запис закону можливий тільки при малих деформаціях). А в анізотропному середовищі маємо записати:
- напруження (але такий запис закону можливий тільки при малих деформаціях). А в анізотропному середовищі маємо записати: 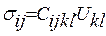
 – тензор напруження;
– тензор напруження;  – тензор модулів пружності;
– тензор модулів пружності;  – тензор деформації. Отже, бачимо, що головна ідея не змінилась, а саме: напруження = константа x деформація.
– тензор деформації. Отже, бачимо, що головна ідея не змінилась, а саме: напруження = константа x деформація.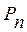 →
→  , Е→
, Е→  , DL/L→
, DL/L→  та перейшли від запису закону Гука в скалярній формі до запису в тензорній.
та перейшли від запису закону Гука в скалярній формі до запису в тензорній. , де ρ - густина середовища; t – вектор коливальних зміщень вузлів кристалічної гратки. Після підстановки виразу для закону Гука у друге рівняння Ньютона, отримуємо хвильове рівняня:
, де ρ - густина середовища; t – вектор коливальних зміщень вузлів кристалічної гратки. Після підстановки виразу для закону Гука у друге рівняння Ньютона, отримуємо хвильове рівняня:  далі шукаємо розв’язок для вектора коливального зміщення вузлів кристалічної гратки необмеженого анізотропного середовища у вигляді плоскої хвилі:
далі шукаємо розв’язок для вектора коливального зміщення вузлів кристалічної гратки необмеженого анізотропного середовища у вигляді плоскої хвилі: 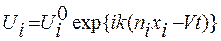 яка поширюється з фазовою швидкістю V, хвильовим числом
яка поширюється з фазовою швидкістю V, хвильовим числом  вздовж напрямку, який визначається напрямляючими косинусами nі (відповідають декартовим осям xі). Оскільки хвиля є плоскою, то зміщення Uі, не змінюються в напрямках, які є перпендикулярними до напрямку поширення хвилі.
вздовж напрямку, який визначається напрямляючими косинусами nі (відповідають декартовим осям xі). Оскільки хвиля є плоскою, то зміщення Uі, не змінюються в напрямках, які є перпендикулярними до напрямку поширення хвилі. або
або 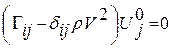 - хвильове рівняння Гріна–Кістофеля яке описує процес поширення пружних хвиль, та в якому введено позначення – тензор Крістофеля:
- хвильове рівняння Гріна–Кістофеля яке описує процес поширення пружних хвиль, та в якому введено позначення – тензор Крістофеля:  .
. (
(  - електростатичний потенціал:
- електростатичний потенціал: 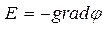 ). Це можливо тому, що Навіть в сильних п’єзоелектриках взаємодія між власними пружними та електромагнітними хвилями є слабою з причини значної різниці швидкостей поширення цих хвиль. Тому поширення цих хвиль розглядають незалежно: пружні коливання розглядаються без врахування електромагнітних ефектів. Отже, в п’єзоелектрику поширюються хвилі, які мають швидкість АХ (а не електромагнітної), а спричинене акустичною хвилею електричне поле подається як градієнт змінного в часі скалярного потенціалу. Властивості п’єзоелектрика враховуються через компоненти п’єзоелектричного тензору ekij. В такому випадку електромагнітна складова цього типу коливань є малою у порівнянні з її пружною складовою.
). Це можливо тому, що Навіть в сильних п’єзоелектриках взаємодія між власними пружними та електромагнітними хвилями є слабою з причини значної різниці швидкостей поширення цих хвиль. Тому поширення цих хвиль розглядають незалежно: пружні коливання розглядаються без врахування електромагнітних ефектів. Отже, в п’єзоелектрику поширюються хвилі, які мають швидкість АХ (а не електромагнітної), а спричинене акустичною хвилею електричне поле подається як градієнт змінного в часі скалярного потенціалу. Властивості п’єзоелектрика враховуються через компоненти п’єзоелектричного тензору ekij. В такому випадку електромагнітна складова цього типу коливань є малою у порівнянні з її пружною складовою. (1)
(1) 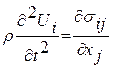 (2)
(2)  (3) Підставимо рівняння (2),(3) в (1) та в рівняння Максвела для діелектриків:
(3) Підставимо рівняння (2),(3) в (1) та в рівняння Максвела для діелектриків:  , та отримаємо:
, та отримаємо:  ,
,  .
.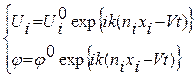 В результаті отримуємо рівняння Гріна-Крістофеля (Хвильове рівняння з урахуванням п’єзоефекту):
В результаті отримуємо рівняння Гріна-Крістофеля (Хвильове рівняння з урахуванням п’єзоефекту): 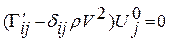 , тут
, тут 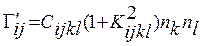 - тензор Гріна-Крістофеля. Тобто врахування п’єзоелектричного ефекту призвело до збільшення ефективних пружних контактів в
- тензор Гріна-Крістофеля. Тобто врахування п’єзоелектричного ефекту призвело до збільшення ефективних пружних контактів в  раз, де
раз, де 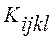 – тензор коефіцієнтів електромеханічного зв’язку.
– тензор коефіцієнтів електромеханічного зв’язку.