 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Технологія Spread Spectrum. Кореляційні властивості сигналів. Коди Баркера, m-послідовності, коди Голда, коди Уолша. Смирнов Є. М
Технологія Spread Spectrum – технологія широкосмугового сигналу, розроблена з метою зниження потужності передавача і підвищення стійкості до вузькосмугових перешкод. Технологія спрямована на перетворення вузькосмугового корисного сигналу в сигнал набагато більш широкого спектра. При цьому спектральна потужність сигналу перерозподіляється по використовуваному частотному діапазону, і максимальна потужність сигналу стає значно нижче початкової. Оскільки використовуваний в широкосмугових системах рівень сигналу порівняний з рівнем природного шуму (noise floor), часто їх називають системами шумоподібного сигналу. Низький рівень сигналу зменшує перешкоди, створювані широкосмуговим
В існуючих на даний час системах цю технологію використовують 3 методи: · Псевдовипадкова перестройка робочої частоти (Frequency Hopping Spread Spectrum, FHSS) Суть методу полягає в періодичній стрибкоподібній зміні несучої частоти за певним алгоритмом, відомим приймачу і передавачу. Станції в кожен момент часу працюють на різних частотах, що дозволяє одночасно працювати великій кількості передавачів. У разі виникнення вузькосмугової перешкоди вона буде спотворювати тільки частину переданого сигналу, що дозволяє говорити про перешкодозахищеність даного методу. Крім того, послідовність стрибків може вибиратися з використанням псевдовипадкової функції, що ускладнює прослуховування переданих даних з боку третіх осіб, приймачі яких не синхронізовані з передавачами. Недоліками методу частотних стрибків є невисока максимальна швидкість передачі, пов'язана з втратами на перемикання між частотами (hop time), і відносно висока потужність передачі на кожній з частот, що може заважати роботі інших передавачів. Перевага методу – простота реалізації. · Метод прямої послідовності (Direct Sequence Spread Spectrum, DSSS) Метод по ефективності перевершує FHSS, але складніше в реалізації. Суть методу полягає в підвищенні тактової частоти модуляції, при цьому кожному символу передаваємого повідомлення ставиться у відповідність деяка досить довга псевдовипадкова послідовність, використовувана для модуляції несучої. Таким чином, один символ (нуль або одиниця) кодується послідовністю з декількох прямокутних імпульсів меншої тривалості. Оскільки ширина спектра прямокутного імпульсу обернено пропорційна його тривалості, передача декількох імпульсів (чіпів) за час, відведений під один імпульс, розширює частотний діапазон. В якості методів перетворення використовуються код Баркера (Barker Code), компліментарний код (Complementary Code Keying, ССК) або метод ортогонального частотного розділення з мультиплексуванням (Orthogonal Frequency Division Multiplexing, OFDM). При прийомі отримана послідовність біт декодується з використанням того ж алгоритму, що і при її кодуванні. Інша пара приймач-передавач може використовувати інший алгоритм кодування - декодування, і таких різних алгоритмів може бути дуже багато. · Метод лінійної частотної модуляції (Chirp Spread Spectrum, CSS). Суть методу полягає в перебудові несучої частоти за лінійним законом. Метод використовується в радіолокації і в деяких радіомодемах. Кореляційні властивості сигналів Кореляційний аналіз послідовностей полягає в кількісному визначенні степені подібності різних сигналів. Автокореляційна функція (АКФ) детермінованого сигналу BS(τ) та взаємокореляційна функція (ВКФ) двох сигналів B12(τ) виражаються формулами:
де Таким чином, при нульовому часовому зсуві автокореляційна функція рівна енергії сигналу Кореляційні властивості розширюючих кодових послідовностей залежать від типу послідовностей, їх довжини, частоти надходження її імпульсів, навіть від її посимвольної структури. Саме за значеннями АКФ та ВКФ вибираються більш ефективні види псевдовипадкових послідовностей (ПВП). Коди Баркера Послідовність Баркера – це ряд, що складається з N елементів
Послідовності Баркера мають мінімальний рівень бокових пелюсток автокореляційної функції, а тому добре підходять для оптимального приймання. Відомі послідовності Баркера мають довжину 2≤N≤13, зокрема, для N=13 код Баркера має вигляд: +1 +1 +1 +1 +1 −1 −1 +1 +1 −1 +1 −1 +1. Коди Баркера мають найкращі серед відомих псевдовипадкових послідовностей властивості шумоподібності (автокореляції), що і зумовило їх широке використання. Ці коди знайшли широке застосування в безпровідних мережах Wi-Fi.
Отже, використання коду Баркера забезпечує можливість передавати сигнал практично на рівні перешкод і до того ж гарантує високу міру достовірності інформації, що приймається. У цьому основний сенс їх вживання. M-послідовності М-послідовності або послідовності максимальної довжини (англ. Maximum length sequence, MLS) – псевдовипадкові послідовності, що знайшли широке вживання в широкосмугових системах зв'язку. Як правило використовуються двійкові М-послідовності члени яких складаються з чисел 1 і 0 або 1 і -1. Такі послідовності володіють наступними властивостями: 1. М-послідовності є періодичними з періодом
2. кількість символів, що набувають значення одиниця, на довжині одного періоду М-послідовності рівного 2n-1, на одиницю більше, ніж кількість символів, що набувають значення нуль. 3. будь-які комбінації символів довжини n на довжині одного періоду М-послідовності за винятком комбінації з n нулів зустрічаються не більше одного разу. Комбінація з n нулів є забороненою: на її основі може генеруватися лише послідовність з одних нулів. 4. сума по mod 2 будь-яких М-послідовностей з її довільним циклічним зрушенням також є М-послідовністю. 5. періодична АКФ будь-якій М-послідовності має постійний рівень бічних пелюсток, рівний (1/N). Коди Голда Коди Голда — тип псевдовипадкових послідовностей. Значимість цих послідовностей полягає у їх дуже низькій взаємній кореляції. Застосовуються в CDMA і GPS. Оптимальні автокореляційні властивості можуть бути отримані і для М-послідовностей, однак, для реалізації принципу колективного доступу необхідний великий набір кодів однакової довжини з хорошими взаємокореляційними властивостями. Тому використовується особливий клас послідовностей, який називають послідовностями Голда. Коди Голда не тільки дозволяють отримати великий набір послідовностей, але також й однорідні та обмежені значення взаємокореляційної функції. Коди Голда добре підходять для використання в якості довгих скремблюючих кодів для бездротового множинного доступу з кодовим поділом каналів. Коди Голда з періодом 2n-1 формуються на основі двох m-послідовностей (а саме підсумовуванням за модулем 2 двох М-послідовностей однакової довжини) з відбором так званих «бажаних пар» (preferred pairs), що мають тризначну функцію автокореляції. Результуючі Коди Голда мають ту ж саму довжину як і вихідні М-послідовності. Коди Уолша
Для матриць є справедливою властивість: кожен рядок є ортогональним будь-якому іншому рядку, а також будь-якому рядку, до якого застосована операція логічного НЕ. Ортогональні коди розширення, такі як послідовності Уолша, можуть використовуватися, тільки якщо всі користувачі одного каналу CDMA синхронізовані з точністю до малої долі елементарного сигналу. Через те, що взаємокореляція різних здвигів послідовностей Уолша не рівна нулю, при відсутності точної синхронізації потрібні псевдовипадкові послідовності.
Поиск по сайту: |
 сигналом для інших передавачів і навпаки – вузькосмугові перешкоди слабко впливають на якість прийому широкосмугового сигналу.
сигналом для інших передавачів і навпаки – вузькосмугові перешкоди слабко впливають на якість прийому широкосмугового сигналу.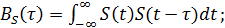

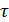 – часовий зсув сигналу. При
– часовий зсув сигналу. При  , маємо
, маємо 
 .
. для
для  , які мають значення +1 та -1 і чергуються так, що виконується умова:
, які мають значення +1 та -1 і чергуються так, що виконується умова: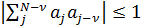 , де
, де  .
. Послідовність Баркера має яскраво виражений автокореляційний пік, відповідний накладенню функції самої на себе. Інші послідовності не мають аналогічної властивості, тобто мають декілька піків кореляції, що значно знижують завадостійкість переданого сигналу.
Послідовність Баркера має яскраво виражений автокореляційний пік, відповідний накладенню функції самої на себе. Інші послідовності не мають аналогічної властивості, тобто мають декілька піків кореляції, що значно знижують завадостійкість переданого сигналу. .
. Код Уолша (Walsh code) – найбільш поширений ортогональний код, що використовується в системі CDMA. Він формується на основі матриці Адамара розмірністю
Код Уолша (Walsh code) – найбільш поширений ортогональний код, що використовується в системі CDMA. Він формується на основі матриці Адамара розмірністю  , де N=0,1,2… Код Уолша довжиною
, де N=0,1,2… Код Уолша довжиною  є рядком матриці Адамара. Принцип формування матриць зображений на рисунку.
є рядком матриці Адамара. Принцип формування матриць зображений на рисунку.