 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Умови еквівалентності аналогових і цифрових систем обробки сигналів. Методи розрахунків цифрових фільтрів. Ляшенко М. І
При цифровій фільтрації потрібно проектувати цифрові фільтри, які еквівалентні аналоговим. Початок проектування цифрового фільтра – вибір відповідного аналогового еквівалентного фільтра. Метод із застосуванням принципу інваріантності імпульсної характеристики. Основною характеристикою аналогового фільтра є
Наступним кроком є одержання імпульсної характеристики з перетворення Лапласа: Умова еквівалентності: Імпульсна характеристика цифрового фільтра є відліками аналогового фільтра. Далі за допомогою z-перетворення знаходимо G(z). Тобто маємо ланцюжок:
G(z) дозволяє спроектувати фільтр. Зауваження: в ланцюжку перетворень можливе спрощення: Розрахунки в обох випадках майже співпадають, тому характеристики фільтра також співпадають. Кожне z визначає порядок фільтра. Іноді пристойна характеристика отримується при врахуванні першого доданку з розкладу в ряд. Інколи процес проектування цифр. фільтра по аналоговому можна спростити. Можливо здійснити частотне перетворення при трансформації аналогового в цифровий. Для цього вводиться поняття цифрової частоти.
Якщо фільтри мали в знаменнику G(z)~1/z-n, фільтри із зворотнім зв'язком. Імпульсна характеристика в часі нескінченна. Такі фільтри наз. фільтрами з нескінченими характеристиками. Якщо вказана залежність відсутня(немає знаменника), то фільтр – з короткою характеристикою. Фільтри з короткою характеристикою завжди стійкі, з нескінченою – можуть бути нестійкі.
Поиск по сайту: |
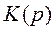 , для визначення якої спочатку необхідно знати АЧХ:
, для визначення якої спочатку необхідно знати АЧХ: 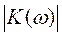 задає смугу, ширину і крутизну. Звідси визначаємо
задає смугу, ширину і крутизну. Звідси визначаємо  , шукаємо полюси розкладу.
, шукаємо полюси розкладу.  - полюси
- полюси 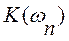 . Тоді маємо шукану функцію у вигляді
. Тоді маємо шукану функцію у вигляді 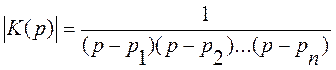 .
. . Далі робиться дискретизація:
. Далі робиться дискретизація: 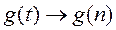 .
.
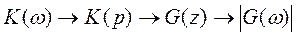 . У вираз для
. У вираз для  →
→  →
→ 
 в даному випадку G(z) буде виражено через lnz. Тому виражаємо логарифм через відповідний ряд:
в даному випадку G(z) буде виражено через lnz. Тому виражаємо логарифм через відповідний ряд: 
 - білінійне наближення. Перевага методу полягає в його в універсальності, за умови відомої
- білінійне наближення. Перевага методу полягає в його в універсальності, за умови відомої  . Нормована частота до частоти дискретизації.
. Нормована частота до частоти дискретизації. 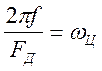 .
.  ,
,  .
. 
 . Користуючись співвідношенням
. Користуючись співвідношенням 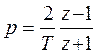 і підставляючи значення для р, отримуємо:
і підставляючи значення для р, отримуємо:  ,
, 

 ,
,
 Так переноситься АЧХ аналогового фільтру і отримується АЧХ цифрового.
Так переноситься АЧХ аналогового фільтру і отримується АЧХ цифрового.