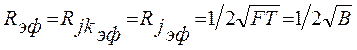|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кореляційні функції сигналів
Оптимальний прийом сигналів здійснюється за допомогою узгоджених фільтрів або кореляторів. Нормований відгук узгодженого фільтра, визначуваного за допомогою інтеграла згортки,
де Uj(t) — сигнал на вході фільтра, узгодженого з сигналом Uk(t)Енергії сигналів з номерами j і k рівні Е,a t — зсув сигналу Uj(t) відносно відгуку Uk(t). При j=k і t=0 ), відкидаючи індекси, маємо
що і визначає нормованість відгуку узгодженого фільтра. Вираз в правій частині (*) визначає інтегральний взаємозв'язок між сигналами Uj(t) і Uk(t) при деякому зсуві t. Якщо t— змінна величина, то rjk(t) — функціонал, що залежить як від функцій Uj(t) і Uk(t) так і від зсуву t. Саме тому rjk(t) називається кореляційною функцією (КФ) сигналів Uj(t) і Uk(t). У залежності від того, узгоджений або не узгоджений сигнал з фільтром, чи є додаткове доплерівське зміщення несучої частоти сигналу, кореляційні функції мають різні представлення. Взаємна функція невизначеності (ВФН) двох сигналів з номерами j і k , по визначенню, виражається через комплексні огинаючі сигналів і через їх спектри таким чином:
де t- зсув за часом між сигналами, Ω — доплерівський зсув частоти. З точністю до малих більш високого порядку нормований відгук узгодженого фільтра пов'язаний з ВФН співвідношенням
Взаємокореляційна функція (ВКФ) є перетином ВФН при W = 0. Вважаючи W=0, отримуємо
Функція невизначеності (ФН). Якщо фільтр узгоджений з сигналом, тобто j=k опускаючи індекс j, отримуємо визначення ФН
Автокореляційна функція (АКФ) — перетин ФН при = 0. Вважаючи W = 0, знаходимо
Видно, що АКФ є перетворенням Фурье енергетичного спектра комплексною огинаючою сигналу. Згідно із зворотним перетворенням Фурье енергетичний спектр
Розглянемо приклад, що ілюструє властивості автокореляційна функції. На мал. 2.8, а, б зображені простий сигнал у вигляді прямокутного імпульсу і його автокореляційна функція. Максимум R(t) приходиться на момент закінчення сигналу t=T. Це пояснюється тим, що R(t) є нормованим напруженням на виході фільтра, узгодженого з вхідним сигналом, максимум якого співпадає з моментом закінчення сигналу, тобто при t=Т максимум R(0) = 1 . Для автокореляційної функції у вигляді трикутного імпульсу, зображеного на мал. 2.8,6, енергетичний спектр (квадрат модуля амплітудного спектра) описується Функцією
Частотна кореляційна функція (ЧКФ) — перетин ФН при t=0. Вважаючи t=0, отримуємо
Вона не залежить від фазової структури сигналу, а визначається тільки квадратом модуля його що огинає. Наприклад, для простого сигналу (мал. 2.8, а) квадрат огинаючої дорівнює 1 (мал. 2.11, а). Тому ЧКФ сигналу, зображеного на мал. 2.8, а записується у вигляді
Вона зображена на мал. 2.11,6. Нулі слідують з. інтервалом 2p/T. Максимум і симетрія кореляційних функцій. Загалом ці функції називаються як було відмічено раніше, кореляційними функціями (КФ). Відомо, що максимум КФ має місце лише при j=k і t=0,W=0, тобто тільки в центрі ФН (або АКФ і ЧКФ). Максимум Rj(0,0)=Rk(0,0)=1 a ,
Властивість симетрії КФ полягає в тому, що
Об'єм і середньоквадратичне значення ВФН і ФН. Відомо, що об'єм, укладений між поверхнею, що описується квадратом модуля ВФН, і площиною невизначеності (або просто об'єм ВФН), рівний одиниці, тобто
і не залежить від форми і номерів сигналів. Вважаючи j=k та відкидаючи індекси, маємо результат: об'єм ФН також не залежить від форми сигналу і рівний одиниці, т. е.
Формули дозволяють знайти ефективні значення ВФН і ФН. Позначимо ця значення через R jk єф , Rєф . Вважаючи, що ВФН. и ФН приблизно розподілені на прямокутнику зі сторонами 2Т і 4pf, можемо записати, що
Видно, що чим більше база сигналу, тим менше ефективні значення.
Поиск по сайту: |
 (*)
(*)
 →
→ 









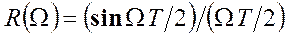



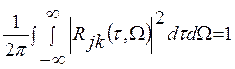

 Звідси знаходимо
Звідси знаходимо