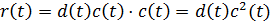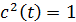|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Системи зв’язку з розширенням спектру. Шумоподібні сигнали. Виграш використання шумоподібних сигналів у стійкості до завад. Загородній В
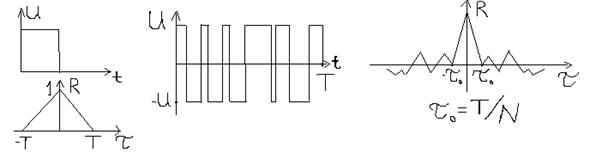
Для характеристики сигналу використовують поняття база Базу сигналу як правило визначають як В=df/N, де df – ширина спектру, а N – швидкість передачі даних у бітах за секунду. Треба відзначити, що такі сигнали не передають за звичай на великі відстані. Отже, в залежності від величини бази сигнали ділять на прості ( Якщо виявлення сигналу в приймачі здійснюється оптимальним чином, то складні сигнали мають переваги в порівнянні з простими, оскільки автокореляційна функція для складних сигналів має чіткий максимум.
Простий та складний сигнал та їх АКФ. При цьому мінімальне відношення сигнал / завада, при якому фільтр лишається узгодженим з сигналом і завадою, визначається:
видно, що для сигналів з великою базою це відношення більше. Тому величину 2В можна назвати коефіцієнтом підсилення шумоподібних сигналів. ШПС мають переваги над простими сигналами, оскільки при дії вузькополосної завади її можна “вирізати” вузькосмуговим селективним фільтром, при цьому інформація ШПС не втратиться.
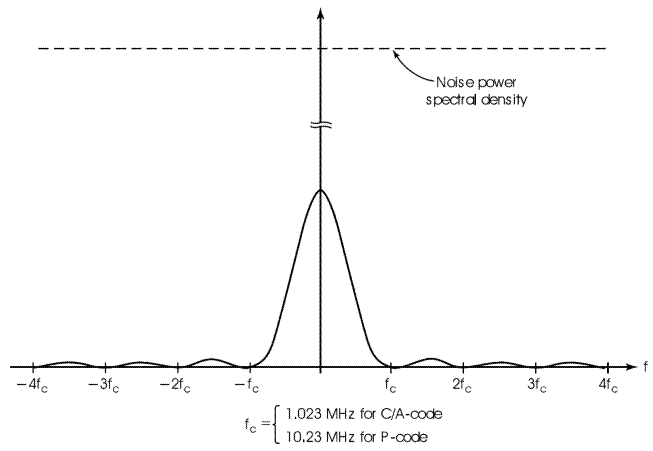
Додаток Основна ідея розширення спектру сигналу – це використання сигналів із гарною автокореляційною функцією. Ми вже знаємо, що використання кореляційного прийому дозволяє ефективно боротися із шумами в каналі зв’язку. Якщо задатися метою розробити сигнал із якомога кращими автокореляційними властивостями, то ми якраз прийдемо до ідеї шумоподібних сигналів. Нам треба придумати такий сигнал, який матиме якомога кращу автокореляційну функцію. Тоді за допомогою корелятора ми зможемо такий сигнал надійно детектувати при прийомі. Але одночасно з тим, дуже бажано, щоб наш сигнал не корелював із іншими сигналами та шумом. Бажані кореляційні властивості шумоподібного сигналу такі: · гарна автокореляція · „гарна“ – чи, точніше – погана кроскореляція Пряме розширення спектру шумоподібним сигналом При DSSS кожен біт корисного сигналу замінюється на послідовність із широким спектром – робиться це множенням. У результаті спектр сигналу розширюється. Спочатку ширина спектру визначалася швидкістю слідування бітів сигналу. Після розширення сигнал займає спектр, що визначається частотою слідування бітів у шумоподібній послідовності. У результаті сигнал після модуляції складається із добутків
Перший множник
Якщо послідовності синхронізовані у часі, то множення знову на ту саму бітову псевдовипадкову послідовність декодує сигнал до попереднього вигляду
Малюнок декодування біту при множенні на той самий сигнал для одиниці та для нуля Спочатку множенням спектр сигналу розширили, а потім таким самим множенням звузили назад. Малюнок у зворотній бік Білет №7
Поиск по сайту: |
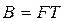 , добуток ширини спектру на його тривалість. Варто зауважити, що F (ширина спектру) не однозначне поняття, як правило за ширину смуги беруть ту частину, в якій зосереджено 99% енергії сигналу.
, добуток ширини спектру на його тривалість. Варто зауважити, що F (ширина спектру) не однозначне поняття, як правило за ширину смуги беруть ту частину, в якій зосереджено 99% енергії сигналу.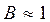 ), на складні (
), на складні (  ) та шумоподібні(ШПС) (
) та шумоподібні(ШПС) ( 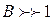 ).
).
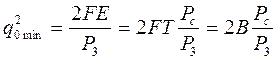
 -потужність сигналу
-потужність сигналу 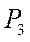 - пот. Завади
- пот. Завади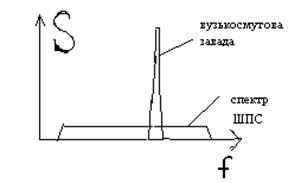

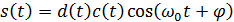
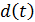 – це оригінальний сигнал,
– це оригінальний сигнал, 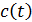 – розширююча послідовність, і останній множник, косинус – це несуча. На приймаючій стороні стоїть пристрій, що звужує спектр сигналу до попереднього вигляду. Фактично це варіант корелятора – сигнал після гетеродина знову множиться на ту саму псевдовипадкову послідовність
– розширююча послідовність, і останній множник, косинус – це несуча. На приймаючій стороні стоїть пристрій, що звужує спектр сигналу до попереднього вигляду. Фактично це варіант корелятора – сигнал після гетеродина знову множиться на ту саму псевдовипадкову послідовність