 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Виведення формули Річардсона-Дешмана
Якщо розташувати вісь Х перпендикулярно поверхні металу, то умова виходу елекрона у вакуум має вигляд: де
Кількість електронів зі складовими швидкостей
Через те, що кожен електрон, що зіштовхується з бар’єром, залишить метал за умови
Для строгого розв’язку задачі про емісію електронів у вакуум треба ввести в це рівняння коефіцієнт прозорості бар’єру
Аналізуємо рівняння далі: через те, що для металів
тобто одиницею в знаменнику можна знехтувати.
де Виразимо тепер енергію через компоненти швидкості з формули
звідки отримаємо:
В
Таким чином:
для Та : тобто складається враження, що Можливою причиною вказаного розходження теорії з дослідом є зміна положення рівня Фермі в металах в залежності від температури. Але при нагріванні металу, як ми знаємо, Е0 змінюється слабо:
де Іншою причиною відмінності Звертаю Вашу увагу на те, що формула є справедливою і для напівпровідників. Лише треба пам’ятати, що
Поиск по сайту: |
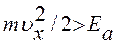 , де
, де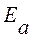 - висота потенціального бар’єру.
- висота потенціального бар’єру.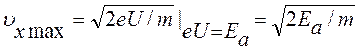 - максимальна швидкість електрона в металі.
- максимальна швидкість електрона в металі. , які підходять кожну секунду до одиниці поверхні металу (потік електронів)
, які підходять кожну секунду до одиниці поверхні металу (потік електронів) (Ця формула отримується з розподілу Фермі-Дірака, коли замість Е поставити m(Vx)2 /2).
(Ця формула отримується з розподілу Фермі-Дірака, коли замість Е поставити m(Vx)2 /2). незалежно від
незалежно від 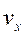 та
та  , то загальна кількість електронів, що здатні залишити метал за одну секунду складе:
, то загальна кількість електронів, що здатні залишити метал за одну секунду складе:
 .
. , де
, де 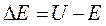 , тобто
, тобто  залежить від співвідношення енергії електрону і висоти потенціального бар’єру. Але через це рівняння дуже важко розв’язати. Тому вводиться поняття
залежить від співвідношення енергії електрону і висоти потенціального бар’єру. Але через це рівняння дуже важко розв’язати. Тому вводиться поняття 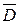 : середнє значення коефіцієнта прозорості потенціального бар’єру для вилітаючих електронів. В такому випадку
: середнє значення коефіцієнта прозорості потенціального бар’єру для вилітаючих електронів. В такому випадку  - одиниці еВ (для вольфраму, наприклад,
- одиниці еВ (для вольфраму, наприклад,  ), а
), а  при Т=3000К, то
при Т=3000К, то ,
,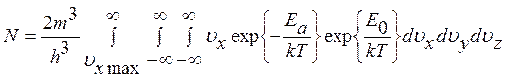 ,
, - повна енергія електрона, який може вийти з дна потенціальної ями.
- повна енергія електрона, який може вийти з дна потенціальної ями.
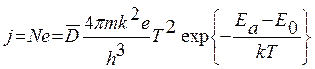
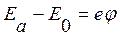
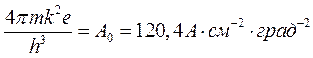

 - стала Зоммерфельда. Для всіх металів вона є однаковою.
- стала Зоммерфельда. Для всіх металів вона є однаковою.  - стала Річардсона-Дешмана. А ось стала Річардсона-Дешмана для різних металів, що знайдена експериментально, в 1,5 ÷ 2 рази менша за
- стала Річардсона-Дешмана. А ось стала Річардсона-Дешмана для різних металів, що знайдена експериментально, в 1,5 ÷ 2 рази менша за  :
: Mo:
Mo:  W :
W : 
 . Теорія вказує на
. Теорія вказує на  , адже вигляд потенціального бар’єру не такий:
, адже вигляд потенціального бар’єру не такий:  , а такий:
, а такий: 
 ,
,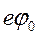 - робота виходу при Т=0К.
- робота виходу при Т=0К. 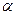 для Mo,Ta та W ‑
для Mo,Ta та W ‑ 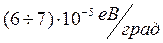 . Тобто при Т=1000К
. Тобто при Т=1000К  .
. 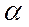 може бути як додатньою, так і від’ємною величиною.
може бути як додатньою, так і від’ємною величиною. від
від 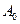 може бути плямистість катоду, яка полягає в тому, що у катода на поверхні є ділянки з різною роботою виходу. Ми ж вимірюємо інтегральний струм емісії.
може бути плямистість катоду, яка полягає в тому, що у катода на поверхні є ділянки з різною роботою виходу. Ми ж вимірюємо інтегральний струм емісії. для напівпровідника – це відстань від рівня Фермі до рівня вакууму:
для напівпровідника – це відстань від рівня Фермі до рівня вакууму:  . Крім того треба пам’ятати, що положення рівня Фермі у напівпровідників набагато помітніше змінюється з температурою.
. Крім того треба пам’ятати, що положення рівня Фермі у напівпровідників набагато помітніше змінюється з температурою.