 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ненасичений і насичений коефіцієнти підсилення активної речовини на одиницю довжини. Закон Бугера в активній речовині. Пугач І. П
Зміну яскравості випромінювання (потужність випромінювання на одиницю площі) при його розповсюдженні в речовині можна описати законом Бугера:
Причому взаємодія випромінювання з речовиною при проходження крізь неї характеризується двома одночасними процесами: резонансна (залежить від частоти) та нерезонансна взаємодія (в широких межах залежить від частоти, але поблизу Нерезонансна взаємодія характеризується коефіцієнтом ρ. Вона не залежить від потужності вхідного випромінювання, описує зміну яскравості непов’язану зі зміною населеностей, а наприклад, з розсіянням. Її існування призводить лише до зменшення потоку, тому до рівняння вона завжди входить зі знаком«-». Резонансна взаємодія характеризуються коефіцієнтом Враховуючи все вищесказане, закон Бугера записується наступним чином: Нас цікавить активне середовище. Розглянемо тільки такі зміни, що пов’язані саме з населеностями (тобто резонансну взаємодію) Можна виразити потужність в елементі об’єму dV через зміни населеностей:
Враховуючи, що У вираз для коефіцієнта підсилення входять населеності i-го та j-го рівнів. Їх значення можна знайти розв’язуючи систему балансних рівнянь для стаціонарних процесів (N – кількість енергетичних рівнів у системі)
В результаті одержали вираз для насиченого коефіцієнта підсилення у активній речовині Насичення виникає в результаті втрат, обумовлених вимушеним випромінюванням в системах з інверсною населеністю. А отже, закон Бугера у диференціальній формі для активних середовищ матиме вигляд:
Оскільки ρ маленьке,
Але якщо є велика інверсія, підсилення може і не бути, зокрема при Стаціонарне значення інтенсивності випромінювання, що поширюється підсилюючою речовиною, встановлюється тоді, коли все, що може випромінити одиничний відрізок довжини активної речовини в режимі повного насичення, поглинається за рахунок нерезонансних втрат в тому ж відрізку. Цей баланс поглинутої та випроміненої енергії призводить до зникнення подальшого підсилення по мірі поширення вздовж підсилювача.
Поиск по сайту: |
 - закон Бугера у диференціальній формі (більш традиційним є запис закону Бугера у інтегральній формі
- закон Бугера у диференціальній формі (більш традиційним є запис закону Бугера у інтегральній формі  , але він справедливий лише за умови, що k не залежить від S або z)
, але він справедливий лише за умови, що k не залежить від S або z) практично відсутня частотна залежність).
практично відсутня частотна залежність). .
.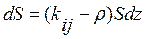 ;
;  (для активного і пасивного середовищ відповідно).
(для активного і пасивного середовищ відповідно). .
.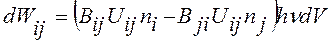
 , то
, то  , і підсилення буде за умови
, і підсилення буде за умови  .Окрім того,
.Окрім того,  (тут s - площа поперечного перерізу елементарного об’єму), а отже
(тут s - площа поперечного перерізу елементарного об’єму), а отже  . Звідки
. Звідки 
 , звідки
, звідки  , де
, де  - визначник системи рівнянь. Завжди можна представити D та Di –таким чином, що вони лінійно залежать від
- визначник системи рівнянь. Завжди можна представити D та Di –таким чином, що вони лінійно залежать від  :
:  ,
,  (це доводиться математично). Тоді
(це доводиться математично). Тоді , і маємо
, і маємо  , де
, де  , оскільки
, оскільки  .
.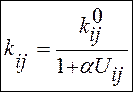 , де
, де  - ненасичена різниця населеностей, α – коефіцієнт нелінійності (показує як населеність піддається насиченню).
- ненасичена різниця населеностей, α – коефіцієнт нелінійності (показує як населеність піддається насиченню). Проаналізуємо одержаний результат. Візьмемо інтеграл від закону Бугера:
Проаналізуємо одержаний результат. Візьмемо інтеграл від закону Бугера:
 →
→

 , де
, де  , та
, та  - яскравість на вході,
- яскравість на вході, 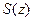 - на виході.
- на виході. , і
, і 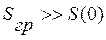 – переходимо до звичної нам форми запису закону Бугера (2):
– переходимо до звичної нам форми запису закону Бугера (2):
 . (3) – це коли
. (3) – це коли  тоді
тоді 