 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вероятность попадания случайной величины, подчиненной нормальному закону на заданный участок ⇐ ПредыдущаяСтр 7 из 7
Известна. случайная величина Х, подчиненная нормальному закону с параметрами mx и σх . Требуется вычислить вероятность попадания случайной величины Х на участок от а до b. Для вычисления этой вероятности воспользуемся формулой
P ( a ≤ X ≤ b) = F ( b ) – F ( a )
где F (x) – функция распределения случайной величины Х .
Сделаем замену переменных
Этот интеграл не выражается через элементарные функции, но его можно вычислить через специальные функции, дающие значения определенных интегралов от выражений Часто применяется т.н. стандартная нормальная функция распределения вида
Эта функция представляет собой функцию распределения для нормально распределенной случайной величины X с параметрами mx = 0 , σх = 1.
Для стандартной нормальной функции распределения Ф* ( х ) составлены таблицы.
  
  
Как и всякая функция распределения, функции Ф*(х) обладает свойствами: 1. Ф*(- ∞) = 0; 2. Ф*(+ ∞) = 1; 3. Ф*( х ) – неубывающая функция . 4. Из симметричности f ( x ) нормального распределения с параметрами mx = 0 и σ = 1 относительно начала координат следует:
Ф* (-x ) = 1 – Ф* ( х ) . Выразим функцию распределения случайной величины Х с параметрами mx и σх через стандартную нормальную функцию распределения Ф* (х). Т.к.
Величина
Вероятность попадания случайной величины Х на участок от а до b :
P ( a ≤ X <b) = F ( b ) – F ( a ) =
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания mx
Связь квадратной нормальной функции распределения, функции Лапласа и интеграла вероятности.
так как
Следовательно, Ф* (х) = 0,5 + Ф ( х )
Ф1 ( х ) =
Ф* (х) = 0,5 +0,5 Ф1 ( х ) = 0,5 ( 1 + Ф1 (х))
Если пользоваться таблицей Ф* ( х ), то
Если пользоваться таблицей Ф1 ( х ) то
Ф1 ( х ) = 2 Ф*(х) – 1.
Правило трех сигм.
Отложим от mx отрезки длиной σ и вычислим вероятность попадания случайной величины в каждый из них.
Т.о. случайная величина с вероятностью 0,9973 находится в интеграле [mx - 3σx, mx + 3σx]. Это значит, что для нормально распределенной случайной величины всё рассеивание ( с точностью до долей процента ) укладывается на участке mx ± 3σx Иначе, вероятность того, что отклонение случайной величины от математического ожидания превысит 3σ, практически равна 0, т.е. это событие считается практически невозможным событием ( т.н. правило трёх сигм). Т.о. зная σ и mx, можно ориентировочно указать интервал возможных значений случайной величины. Из правила трёх сигм вытекает также ориентировочный способ определения σ : берут максимальное практически возможное отклонение от среднего и делят его на 3.
Кроме нормального распределения и равномерного широко используют другие типы распределений случайных величин.
Поиск по сайту: |

 ; х = σхt + mx ; dx = σx dt.
; х = σхt + mx ; dx = σx dt. , где
, где  .
. или
или  , для которых составлены таблицы. Существует много разновидностей этих функций.
, для которых составлены таблицы. Существует много разновидностей этих функций.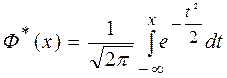 .
.

 ,
,
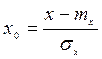 - называется нормированной случайной величиной, для которой M [x0] = 0 , а D[x0] = 1.
- называется нормированной случайной величиной, для которой M [x0] = 0 , а D[x0] = 1. .
.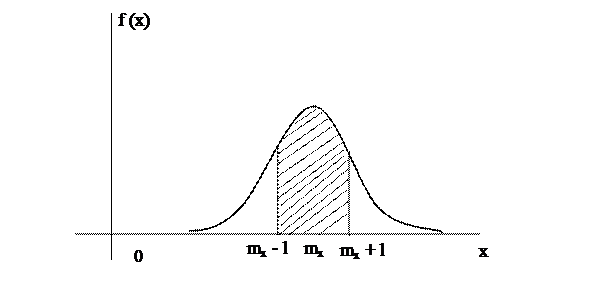


 т.к.
т.к.  , то
, то  ,
,
 =
= 


 = 2 Ф ( х )
= 2 Ф ( х ) .
. .
.


