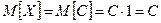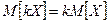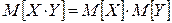|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математическим ожиданием случайной величины Х называется её среднее значение
Рассмотрим дискретную случайную величину Х. Предположим, что проводится серия из N независимых испытаний, в каждом из которых случайная величина Х принимает определённое значение. Пусть значение х1 появилось m1 раз х2 -//- m2 ………………………………… хn mn раз
Здесь m1 + m2 +……. + mn = N
Среднее арифметическое значение величины Х или выборочное среднее
При неограниченном увеличении числа опытов N частота При достаточно большом числе независимых опытов
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятность этих значений В случае когда В иностранной литературе, математическое ожидание величины Х обозначают ЕХ от английского expected value (ожидаемое значение ).
Для непрерывной случайной величины
где f (x) – плотность распределения величины Х
Свойства математического ожидания. 1. Математическое ожидание неслучайной величины С равно этой постоянной (математическое ожидание неслучайной величины равно самой величине). Постоянную С можно рассматривать как случайную величину Х, которая может принимать только одно значение С с вероятностью равной единице. Поэтому
2. Постоянный множитель можно выносить за знак математического ожидания, т.е.
Докажем для дискретных СВ
3. Математическое ожидание суммы нескольких случайных величин любого типа равно сумме математических ожиданий этих величин (без доказательства).
4. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению математических ожиданий этих величин (без доказательства).
Под суммой ( произведений) двух случайных величин Х и Y понимают случайную величину Z = X + Y ( Z = X · Y) , возможные значения которой состоят из сумм ( произведений) каждого возможного значения величины Х и каждого возможного значения величины Y.
Если x1 , x2 …..xn – независимые СВ то математическое отклонение их произведения равно произведению их математических ожиданий.
Поиск по сайту: |
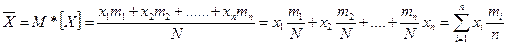
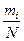 - частота или статистическая вероятность события Х = хi – обозначим ее
- частота или статистическая вероятность события Х = хi – обозначим ее 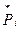
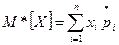
 будет сходиться по вероятности к вероятности Pi.
будет сходиться по вероятности к вероятности Pi. сходит по вероятности к математическому ожиданию
сходит по вероятности к математическому ожиданию  (одна из форм закона больших чисел).
(одна из форм закона больших чисел). Случайная величина
Случайная величина 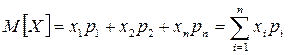
 надо обозначить одной буквой, будем писать
надо обозначить одной буквой, будем писать 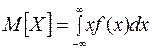 ,
,