 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Cвойства функции распределения
Дадим геометрическую интерпретацию функции распределения:
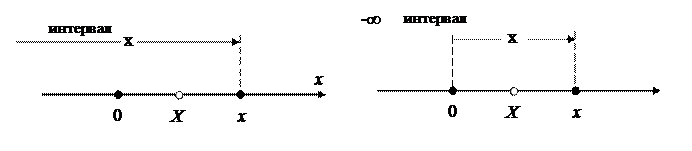 Будем рассматривать СВ Х как случайную точку Х на оси Ох, которая в результате опыта может занять то или иное положение. Тогда F(x) есть вероятность того события, что случайная точка Х в результате опыта попадёт левее точки х, где т.е.
F(x) = Р (- ∞≤ Х < х).
1)Будем увеличивать х, т.е. перемещать точку х вправо по оси абсцисс. При этом вероятность того, что случайная точка X попадёт левее х, не может уменьшиться. Функция распределения F(x) есть неубывающая функция своего аргумента, т.е. при х2 > х1 F ( x2 ) ≥ F ( x1 ).
2)Будем неограниченно перемещать точку х влево по оси абсцисс. При этом попадание случайной точки Х левее х в пределе ставится невозможным событием, а следовательно вероятность этого события стремится к нулю. На минус бесконечности функция распределения равна нулю
F (- ∞ ) = 0.
3) На плюс бесконечности функция распределения равна 1
F ( + ∞ ) = 1.
Неограниченно перемещая точку х вправо, убеждаемся в этом свойстве, т.к. событие Х < х становится достоверным.
Существует ещё т.н. непрерывно – дискретная смешанная СВ, возможные значения которой непрерывно заполняют некоторый промежуток , но для которых функция распределения не везде является непрерывной, а в отдельных точках держит разрывы ( например выработка мощности несколькими агрегатными станциями).
Вероятность попадания случайной величины на заданный участок.
Условимся левый конец а включать в участок ( а, b ), а правый b не включать. Тогда попадания СВ Х на участок
а ≤ Х < b
Выразим вероятность этого события через функцию распределения F (x). Рассмотрим три события: А, состоящее в том, что Х< b В, состоящее в том, что Х< а С, состоящее в том, что а ≤ Х< b
Событие А = В + С , где события, В и С– несовместные события. По правилу сложения вероятностей P ( X < b ) = P ( X < a) + P (a ≤ X < b ) P (a ≤ X < b ) = F ( b ) – F ( a )
Вероятность попадания случайной величины на заданный участок равна разности значений функции распределения на концах этого участка.
P Если СВ и F(x) в точке а непрерывна, то вероятность того, что непрерывная СВ примет заданное значение, равна нулю. P (a < X < b ) = P (a ≤ X < b ) = P (a < X ≤b ) Если СВ дискретна, то Р ( Х= а ) = Р Функция распределения вероятностей является исчерпывающей характеристикой СВ. Две СВ с одинаковыми функциями распределения называются эквивалентными.
Поиск по сайту: |
Это событие заключается в том, что СВ примет значение, заключенное в некоторых пределах, например от а до b, где (а< b)
равносильно выполнению неравенства
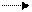Будем неограниченно уменьшать участок 
,