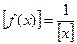 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Плотность распределения вероятностей
Если функция распределения F (x) везде непрерывна, а следовательно и СВ Х непрерывна и имеет производную, то производная от функции распределения СВ называется плотностью распределения вероятностей непрерывной СВ Х. График плотности f ( x ) называется кривой распределения.
Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения по 2 отличиям от ФР.
Плотностью вероятности ( или плотностью распределения или просто плотностью) непрерывной случайной величины Х называется производная функции распределения
по независимой переменой х.
Будем считать, что плотность распределения существует только для непрерывных случайных величин.
Рассмотрим непрерывную СВ Х с плотностью распределения f(x) и элементарный участок dx, примыкающий к точке х.
Вероятность попадания случайной величины Х на элементарный участок dx равна f (x) dx.
f (x) dx – элемент вероятности.
Выразим вероятность попадания случайной величины Х на отрезок от а до b через плотность распределения. Она равна сумме элементов вероятности на всём этом участке, т.е. P (a ≤ X < b ) =
Геометрически P (a ≤ X < b ) равна площади кривой распределения, опирающейся на этот участок.
Выразим функцию распределения через плотность. По определению
F (x) = P ( X< x ) = P (- ∞ ≤ X < x)
отсюда имеем
Геометрически F (x) есть площадь кривой распределения, лежащая левее точки х.
Свойства плотности распределения. 1. Плотность распределения – неотрицательная функция.
т.к. F (x) – неубывающая.
2. Это следует из F (x) =
3. F (x) – величина безразмерная f (x) – имеет размерность, обратную размерности случайной величины, т.е.
Числовые характеристики случайных величин. Функция или плотность распределения полностью определяет распределение случайной величины. Однако в ряде задач достаточно использовать более простые характеристики случайной величины. Назначение числовых характеристик: в сжатой, компактной форме выразить существенные черты распределения. Одной из таких характеристик является среднее значение случайной величины или математическое ожидание.
Поиск по сайту: |
= 
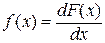
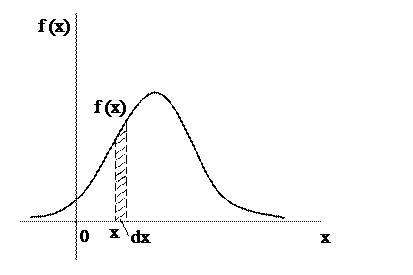
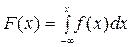
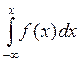и из того, что 
