Описание второй подсистемы

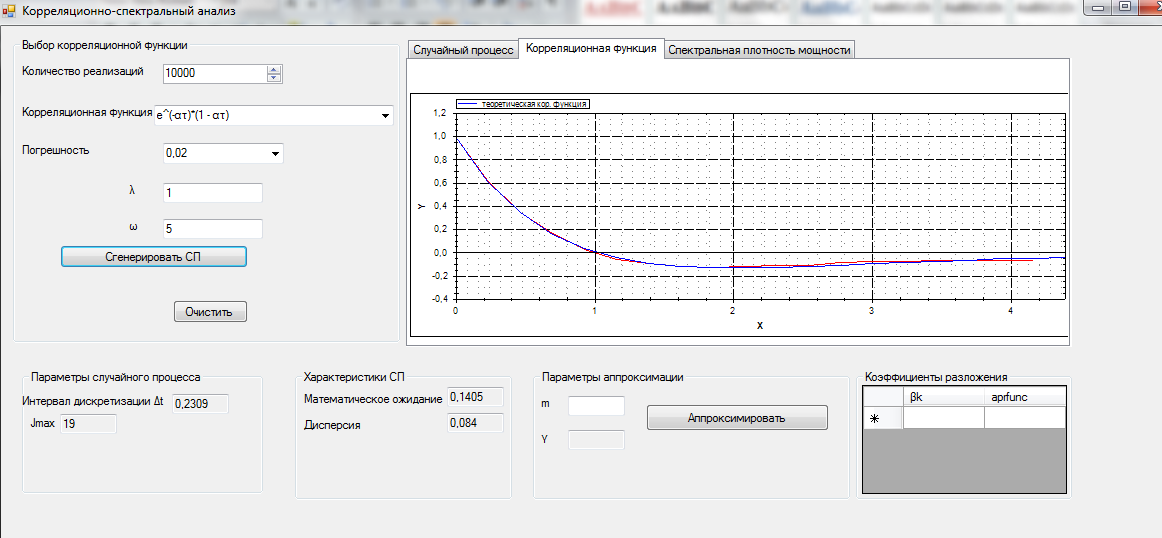
Переходя по вкладкам, пользователь может перейти ко второй подсистеме и посмотреть вероятностную характеристику случайного процесса - построение КФ, причем на графике отображаются как практическая, так и теоретическая КФ (рисунки 11 - 14)

Рисунок 11 – Визуализация вероятностной характеристики СП – КФ (модель 1)

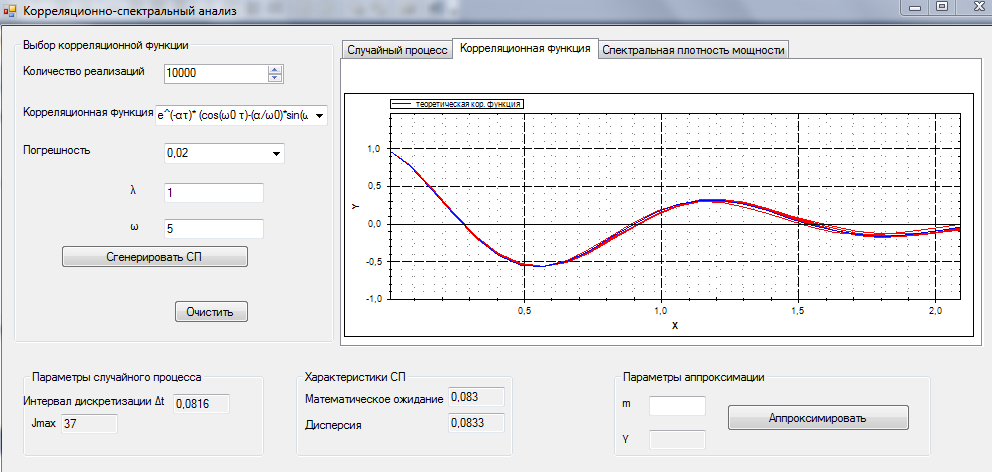
Рисунок 12 – Визуализация вероятностной характеристики СП – КФ (модель 2)

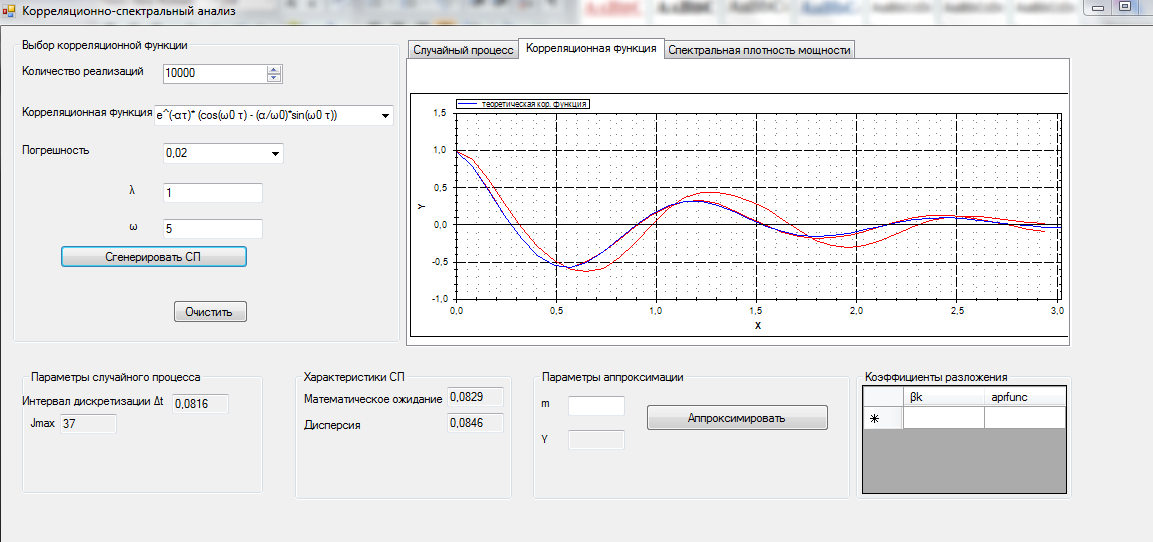
Рисунок 13 – Визуализация вероятностной характеристики СП – КФ (модель 3)

Рисунок 14 – Визуализация вероятностной характеристики СП – КФ (модель 7)

Благодаря второй подсистеме, пользователь может наблюдать «разброс» результатов при очередной генерации СП (рисунок 15)

Рисунок 15 – Визуализация вероятностных характеристик СП – КФ, при многократной генерации СП

Так же вторая подсистема позволяет наблюдать разницу в результатах в зависимости от количества отсчетов и погрешности (рисунки 16, 17)

Рисунок 16 – КФ, при количествах отсчетов 100 и 10000

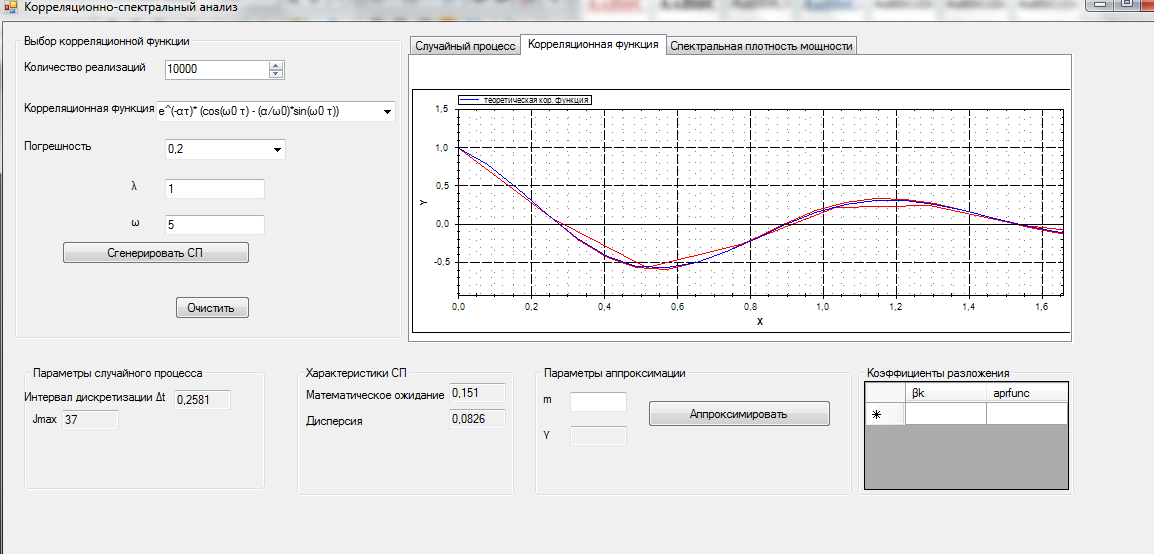
Рисунок 17 – КФ, при погрешностях 2% и 20%

Так же пользователь может построить ортогональную модель корреляционной функции в базисе Якоби [-1/2;0]. На экранную форму в виде таблицы выводятся рассчитанные коэффициенты, использованные для построения модели и график аппроксимированной корреляционной функции (рисунок 18)

Рисунок 18 – Ортогональная модель КФ

Путем изменения порядка и параметра масштаба можно сделать более точное построение ортогональной модели корреляционной функции, при этом пользователь вводит значение порядка, и система рассчитывает и выводит оптимальное значение параметра масштаба (рисунок 19)

Рисунок 19 – Ортогональная модель КФ при значениях m 10 и 30

Описание третьей подсистемы

Перемещаясь далее по вкладкам, пользователь может перейти к третьей подсистеме и оценить графическую интерпретацию спектральной плотности мощности случайного процесса, путем сравнения с теоретической

Рисунок 20 – Спектральная плотность мощности СП

Так как пользователь самостоятельно задает количество членов ряда, в третьей подсистеме можно посмотреть зависимость результатов от этой величины, путем наложения графиков, полученных при разных значениях параметра m (рисунок 21)

Рисунок 21 – Спектральные плотности мощности СП, при разных значениях параметра m

Выбор и обоснование конструкторско-технологических средств

Поиск по сайту: