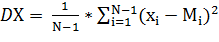|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вероятностные и числовые характеристики
Для реализации поставленной задачи на ЭВМ необходимо спроектировать дискретную систему, так как невозможно реализовать непрерывную. Для этого введем понятие дискретной СВ. Рассмотрим СВ X, возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, Пусть задана функция f(x), значение которой в каждой точке x = xi , (i=1,2,…n) равно вероятности того, что величина X примет значение xi f(xi) = f(X= xi) Такая СВ X называется дискретной (прерывной). Функция F(х) называется законом распределения вероятностей СВ. Эта функция определена в точках последовательности x1, x2, ..., xn, ... .Так как в каждом из испытаний СВ X, принимает всегда какое-либо значение из области ее изменения, то f(x1)+f(x2)+…+f(xn)+… = 1 В рамках поставленной задачи дискретизация осуществляется по времени.
Рисунок 2 – Дискретизация по времени Рассмотрим основные числовые характеристики СП. Число x1f1 +x2f2 + ... xnfnназывается математическим ожиданием(МО) дискретной СВ X,имеющей распределение f(X = хi) = fi (i = 1,2,..., n), и обозначается символами MX. Таким образом, по определению,
Основные свойства МО: МО константы равно этой константе: M(c) =c ; МО – линейный функционал на пространстве случайных величин, т.е. для любых двух СВ x, h и произвольных постоянных a и b справедливо: M(ax + bh ) = a M(x )+ b M(h ); МО произведения двух независимых СВ равно произведению их МО: M(x h ) = M(x )M(h ). МО квадрата отклонения СВ X от её математического ожидания называется дисперсиейСВ X и обозначается символом DX. Таким образом, по определению, DX = M [(Х - MX)2 ] или Основные свойства дисперсии: дисперсия любой СВ неотрицательна: Dx > 0; дисперсия константы равна нулю, Dc=0; для произвольной константы D(cx ) = c2D(x); дисперсия суммы двух независимых СВ равна сумме их дисперсий: D(x ± h) = D(x) + D (h). МО и дисперсия являются частными случаями следующих более общих понятий - моментов СВ. Пусть k - натуральное число. МО k-ой степени СВ X называется начальным моментомпорядка kвеличины X и обычно обозначается через αk. Т.о., по определению, αк =M(Xk ). В частности, αk=MX. Для дискретной СВ начальный момент αk выражается суммой:
МО СВ |x —MX|k, где k - натуральное число, называется абсолютным центральным моментом k-го порядка СВ X и обычно обозначается черезμk.Таким образом, по определению: μk = M(|Х-МХ| k). Выше было рассмотрено определение корреляционной функции для двух аргументов (см пункт 1.1.2): Кх(t1,t2) = M [Ẋ (t1) Ẋ (t2)]. Его можно привести к функции одного аргумента, взяв некоторый фиксированный интервал между сечениями. Тогда получим: Kx(τ) = M[Ẋ (t) Ẋ (t + τ)].
Поиск по сайту: |