 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методы моделирования СП
Метод рекурсивной фильтрации Часто при решении задач имитационного моделирования средств измерений возникает необходимость в формировании процессов с заданным видом корреляционной функции. При этом не обращают внимания на закон распределения процесса. Теоретически эта задача решается методом фильтрации и сводится к определению характеристик формирующего фильтра при известных характеристиках входного и выходного сигналов (рисунок 1). Поиски более быстродействующих алгоритмов моделирования СП с заданным видом корреляционной функции привели к использованию рекурсивной фильтрации:
Рисунок 1 – Схема рекурсивного фильтра Для нахождения коэффициентов aiи bi(т.е. параметров фильтра) применяются, в основном, три класса методов: методы преобразования аналоговых фильтров в цифровые, прямые методы расчета цифровых фильтров в Z-плоскости и методы, использующие алгоритмы оптимизации. В общем случае невозможно отдать предпочтение какому-либо одному из них. С учетом применимости этих методов в конкретных условиях и многих других факторов, каждый из них может оказаться наиболее подходящим. Однако большинство цифровых фильтров рассчитываются методом билинейного преобразования стандартных аналоговых фильтров. Это обстоятельство связано с тем, что в задачах статистического моделирования необходимо проектировать фильтры, для которых билинейные преобразования аналоговых фильтров уже известны. Следует отметить два препятствия на пути осуществления намеченного выше подхода к моделированию СП. Первое состоит в том, что далеко не всегда бывают, заданы любые конечномерные распределения СП. Второе – в том, что даже если любые конечномерные распределения заданы, для больших пформирование реализаций случайного вектора становится громоздким и неудобным для использования на электронных цифровых вычислительных машинах. Эти обстоятельства заставляют использовать для моделирования либо специфические свойства процессов, относящихся к тем или иным классам СП, либо возможность представления данного процесса через более простые случайные элементы. В рамках курсового проекта для первой модели используется следующий алгоритм:
где А для седьмой модели:
где
Поиск по сайту: |
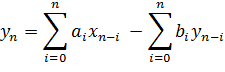
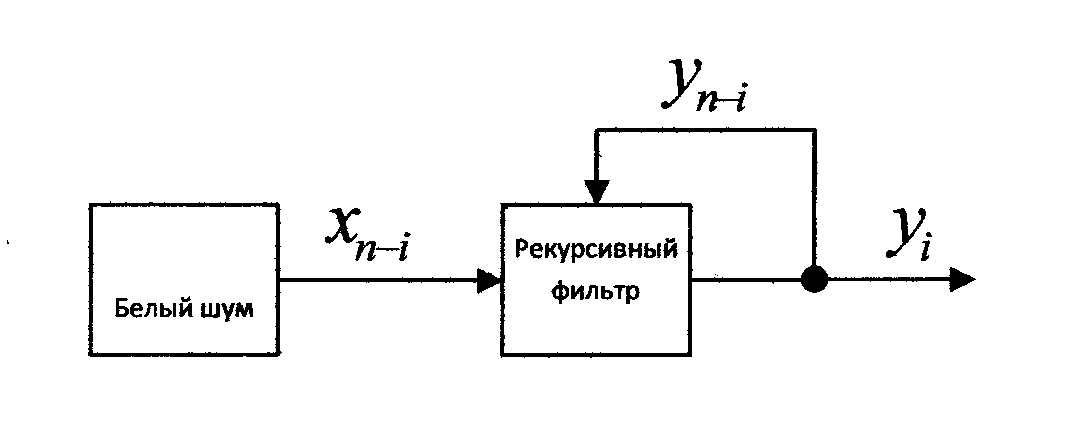
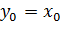 ;
; 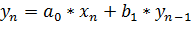 ,
, ;
; 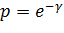 ;
;  ;
; 
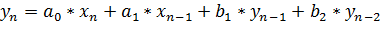 ,
,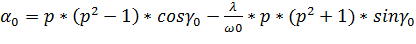 ;
;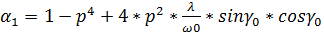 ;
;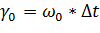 ;
; ;
;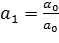 ;
;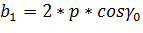 ;
;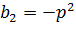 [6].
[6].