 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Аппроксимация корреляционных функций ортогональными функциями
Одной из сложных задач, которую приходится решать при аппроксимации КФ, является выбор модели КФ. Одним из решений этой задачи является применение разложения корреляционной функции в ряд по той или иной системе ортогональных функций. Математическим обоснованием этого метода является теорема Мерсера, согласно которой симметричная и положительно определенная функция, которой и является функция корреляции, может быть разложена в равномерно и абсолютно сходящийся ряд вида:
где
Это семейство характеризуется интегралом:
Так как ряд сходится на интервале (
В качестве системы базисных функций применяются ортогональные функции Лагерра, Лежандра, Хаара и т. д. Выбор системы базисных функций зависит, в основном, от возможности представления КФ минимальным числом членов разложения для типовых моделей, удобством в работе. В рамках курсового проекта в качестве системы базисных функций были использованы функции Якоби [-1/2;0], которые являются одной из распространенных систем ортогональных функций определяемые выражением:
Следует подчеркнуть, что на практике приходится ограничиваться конечным числом ряда Тогда для модели корреляционной функции
определяются формулой: При оценке коэффициентов разложения ряда, для вычисления применялся следующий метод:
Где
Для ортогонального базиса Якоби [-1/2;0]:
Параметры масштаба для ортогональных функций определяются по формулам: для 1 модели: Значение интервала дискретизации
В рамках поставленной задачи Значение интервала дискретизации можно рассчитать по формулам: для первой модели КФ а для седьмой модели КФ Число интервалов дискретизации:
Минимальное количество требуемых ординат корреляционной функции
Поиск по сайту: |
 ;
; - коэффициенты Фурье;
- коэффициенты Фурье; – семейство базисных функций, ортонормированных в интервале (
– семейство базисных функций, ортонормированных в интервале (  ) с весом μ (τ).
) с весом μ (τ).
 .
. .
. , имеющие ограниченное число параметров, коэффициенты разложения, вызывающие минимум квадратической погрешности аппроксимации:
, имеющие ограниченное число параметров, коэффициенты разложения, вызывающие минимум квадратической погрешности аппроксимации: ,
, .
.
 ,
,  .
.




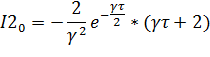

 . [7]
. [7] , для 7 модели:
, для 7 модели: 
 рассчитывается .
рассчитывается . , где δ – заданная допустимая погрешность
, где δ – заданная допустимая погрешность - максимальное по модулю значение второй производной соответствующей функции
- максимальное по модулю значение второй производной соответствующей функции ,
,
 [5].
[5]. и значение интервала дискретизации
и значение интервала дискретизации