 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задание № 10. Расчет пластины методом Ритца ⇐ ПредыдущаяСтр 5 из 5
Для прямоугольной пластины, загруженной равномерно распределенной нагрузкой интенсивностью q и сосредоточенной силой величиной F, расположенной в точке K с координатами xF, yF при заданном выражении функции прогибов требуется: 1) установить условия опирания пластины; 2) методом Ритца определить коэффициент C; 3) построить эпюры прогибов для указанных сечений пластин; 4) построить эпюры изгибающих моментов, поперечных сил, крутящих моментов; 5) построить эпюры нормальных и касательных напряжений для указанных сечений. Расчетная схема плиты приведена на рис. 9.
Рис. 9
Из табл. 12 требуется выбрать функцию прогибов, удовлетворяющую граничным условиям на гранях пластины, т.е.
w(x,y) = C ×f i (x)×j j (y),
где i – номер функции в направлении оси х; j – номер функции в направлении оси y.
Цилиндрическая жесткость Эпюры внутренних усилий построить по формулам:
Эпюры строить, исходя из того, что в заданном сечении пластины ее длину и ширину разделить на четыре части. Эпюры напряжений в заданной точке пластины по ее толщине построить согласно формулам:
где z – расстояние по толщине пластины от ее нейтральной плоскости до точки, в которой определяется напряжение. Исходные данные для расчета следует принять по табл. 13.
Таблица 12 Функции прогибов
Таблица 13 Исходные данные к заданию № 10
Задание № 11. Расчет балки на сплошном Упругом основании Для балки, лежащей на сплошном упругом основании требуется определить внутренние усилия и перемещения, используя соответствующие уравнения метода начальных параметров. Работа выполняется в два этапа. На первом этапе необходимо записать уравнения деформаций и внутренних усилий для каждого участка балки. Напряженно-деформированное состояние балки, лежащей на сплошном упругом основании, зависит от жесткостных характеристик балки и упругого основания. Этими характеристиками являются: EJz – изгибная жесткость балки;
где Е – модуль упругости материала балки, кН/м2; Jz – момент инерции поперечного сечения балки, м4; K0 – коэффициент податливости упругого основания, зависящий от свойств грунта, кН/м3; b – ширина поперечного сечения балки, м. При расчете методом начальных параметров начало координат выбирается в крайней левой точке балки. Поскольку реакция упругого основания изменяется непрерывно по длине балки, то для построения криволинейных эпюр деформаций и внутренних усилий необходимо определить их значения для нескольких точек по длине. Начальные параметры зависят от граничных условий. В табл. 14 представлены уравнения в зависимости от действующих внешних нагрузок. В этих уравнениях y0, j0, M0, Q0 – начальные параметры, из которых два всегда равны нулю (табл. 15). Неизвестные начальные параметры определяются из условий закрепления правого края балки. В уравнения y, j, M, Q (табл. 14) входят функции Y1(x), Y2(x), Y3(x), Y4(x), названные функциями Крылова-Коши, значения которых определяются в зависимости от аргумента bx, где x – координаты точек балки в принятой системе координат:
Y1(x) = chbx × cosbx; Y2(x) = 0,5(chbx × sinbx + shbx × cosbx); Y3(x) = 0,5shbx × sinbx; Y4(x) = 0,25(chbx × sinbx – shbx × cosbx).
В зависимости от характера действующих нагрузок и от условий закреплений левого конца балки для каждого участка необходимо записать уравнение по форме, представленной в табл. 14. Поскольку при составлении уравнений для различных сечений каждый раз рассматривается часть балки слева от сечения, то в уравнение для каждого последующего сечения входят все слагаемые уравнения в предыдущих сечениях. Поэтому запись уравнений для любого сечения может быть представлена в виде табл. 16.
Поиск по сайту: |

 .
.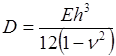 .
.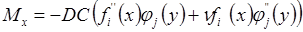 ;
; ;
;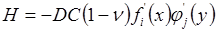 ;
;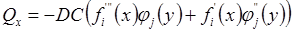 ;
;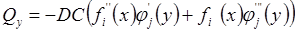 .
.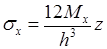 ;
; ;
; ,
,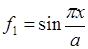
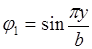
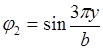
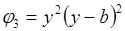




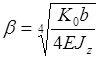 – коэффициент жесткости,
– коэффициент жесткости,