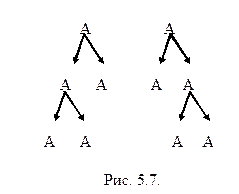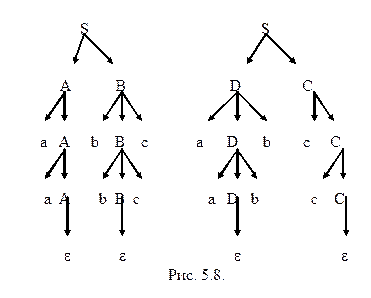Неоднозначность КС-грамматик и языков

Напомним, что КС-грамматика G неоднозначна, если существует цепочка aÎL(G), имеющая два или более различных деревьев вывода. Если грамматика используется для определения языка программирования, желательно, чтобы она была однозначной. В противном случае программист и компилятор могут по разному понять смысл некоторых программ. Неоднозначность - нежелательное свойство КС-грамматик и языков.

Пример неоднозначной КС-грамматики арифметических выражений был рассмотрен в разделе 1.1. Но самый известный пример неоднозначности в языках программирования - это “кочующее else”.

Пример 5.5. Рассмотрим грамматику с правилами вывода

S ® if b then S else S½ if b then S½a

Эта грамматика неоднозначна, так как цепочка

if b then if b then a else a

имеет два дерева вывода, первое из которых (рис 5.6. (а)) предполагает интерпретацию

if b then (if b then a) else a ,

а второе (рис 5.6 (б))-

if b then (if b then a else a)

–

Хотелось бы иметь алгоритм, который по произвольной КС-грамматике выяснял, однозначна она или нет. Но, к сожалению, можно доказать, что проблема, однозначна ли КС-грамматика G, алгоритмически неразрешима. Хотя такого алгоритма нет, можно указать некоторые встречающиеся в правилах конструкции, приводящие к неоднозначности, которые можно распознать на практике и избегать при описании языков программирования.

Грамматика, содержащая правила A ® AA½a , неоднозначна, так как подцепочка AAA допускает два различных разбора (рис. 5.7).

Здесь можно устранить неоднозначность, если вместо предложенных правил с двухсторонней рекурсией использовать одностороннюю, то есть использовать правила A ® AB½B и B ® a или правила A ® BA½B и B ® a.

Другой пример неоднозначности - правило A ® AaA , так как цепочку AaAaA можно получить по двум разным деревьям вывода. Пара правил A ® aA½Ab тоже создает неоднозначность, - цепочка aAb имеет два разных левых вывода A Þ aA Þ aAb и A Þ Ab Þ aAb.

Все перечисленные примеры, так или иначе, связаны с двухсторонней рекурсией. Более тонкий пример - пара правил A ® aA½aAbA , по которым цепочка aaAbA имеет два вывода A Þ aAbA Þ aaAbA и A Þ aA Þ aaAbA . Если при двухсторонней рекурсии средством борьбы с неоднозначностью является устранение рекурсии с одной из сторон, то в последнем случае поможет левая факторизация.

Из приведенных примеров ясно, что определенная выше неоднозначность - это свойство грамматики, а не языка. Для некоторых неоднозначных грамматик можно построить эквивалентные им однозначные грамматики.

Пример 5.6.Рассмотрим грамматику из примера 5.5. Эта грамматика неоднозначна потому, что else можно ассоциировать с двумя различными then. Неоднозначность можно устранить, если связать else с последним из предшествующих ему then, как на рис. 5.6 (б). Для этого введем два нетерминала S₁ и S₂ с тем, чтобы S₂ порождал только полные операторы вида if-then-else, а S₁ - операторы обоих видов. Правила новой грамматики имеют вид

S₁ ® if b then S₁½if b then S₂ else S₁½a

S₂ ® if b then S₂ else S₂½a

Тот факт, что слову else предшествует только S₂ , гарантирует появление внутри конструкции then-else либо символа a, либо другого else. Таким образом, структура, изображенная на рис. 5.6 (а), здесь не возникает. –

КС-язык называется неоднозначным (или существенно неоднозначным), если он не порождается никакой однозначной КС-грамматикой.

С первого взгляда не видно, существуют ли вообще неоднозначные КС-языки, но нашим следующим примером и будет такой язык.

Пример 5.7. Пусть L= {a ⁱ b ^j c ^k ½i = j или j = k}. Этот язык неоднозначен, что можно строго доказать. Интуитивно же это объясняется тем, что цепочки с i = j должны порождаться группой правил, отличных от правил, порождающих цепочки с j = k. Тогда, по крайней мере некоторые из цепочек с i = j = k должны порождаться обеими механизмами. Одна из КС-грамматик, порождающих L, такова:

S ® AB½DC

A ® aA½e

B ® bBc½e

C ® cC½e

D ® aDb½e

Ясно, что она неоднозначна и на рис. 5.8 представлены два дерева вывода цепочки aabbcc. Проблема, порождает ли данная КС-грамматика однозначный язык (т.е. существует ли эквивалентная ей однозначная грамматика), алгоритмически неразрешима. Но для некоторых больших подклассов КС-языков известно, что они однозначны. Именно к этим подклассам и относятся все созданные до сих пор языки программирования.

Поиск по сайту: