 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Исключение тупиковых правил из грамматик
Правило A® j By называется внешним тупиком, если не существует правила B®x . (Из нетерминала B нет выхода). Правило B® x называется внутренним тупиком, если B ¹ S и не существует правила A® j By. (Нетерминал B не может появиться ни в одной сентенциальной форме, выводимой из начального символа грамматики. Внутренний тупик - это аналог недостижимого состояния конечного автомата). Циклический тупик - это группа правил вида A0® j1A1y1 A1® j2A2y2 .................. An® j0A0y0 , где Ai ¹ S и при этом либо для любого Ai не существует правил вида B® lAim (циклический тупик внутреннего типа), либо для любого Ai не существует правил вида Ai®c (циклический тупик внешнего типа). ƒ Теорема 4.5. Для любой грамматики существует эквивалентная ей грамматика без тупиков. Для доказательства данной теоремы достаточно вспомнить, что эквивалентные грамматики порождают один и тот же язык (множество терминальных цепочек, которое выводятся из начального символа грамматики). Очевидно, что правила, включающие тупики, при порождении терминальных цепочек из начального символа грамматики просто не могут использоваться. Алгоритмы поиска тупиков и их устранения рассмотрим на примере. Пример 4.4. Пусть задана грамматика c начальным символом S и следующим множеством правил S® a A½c C½b D½q P½k T A® c C C® k T® m D® b T½f K P® c R R® d K B® d Q½m Q® p B½r B. Здесь выбрана автоматная грамматика только для того, чтобы наглядно проиллюстрировать ее графом состояний (рис. 4.1). Построим новую грамматику, отбирая из исходной “хорошие” (производящие нетерминалы), из которых выводится терминальная цепочка. Для этого положим, что множество X0 = VT , ,то есть X0 совпадает с множеством терминалов. X1 = { A | $ A® x , где xÎ Xo} , то есть те нетерминалы, из которых терминальная цепочка получается за один шаг.
X2 = { A | $ A® x , где xÎ ( Xo È X1 ) } , ....................................................... Xi = { A | $ A® x , где xÎ
то есть Xi - множество нетерминалов, из которых терминальная цепочка получается не более, чем за i шагов (под шагом здесь понимается одновременная замена всех нетерминалов сентенциальной формы). На каждом шаге мы добавляем новые нетерминалы, их конечное число, следовательно конечен и данный процесс ( X1 Í X2 Í ... X i Í VN ). Положим Z i равным разности X i и X i-1 ,Z i = X i \ X i-1 - это те нетерминалы, из которых терминальная цепочка получается ровно за i шагов. Если Z i = Æ, - пустое множество, то процесс формирования продуктивных нетерминалов пора закончить, так как из Z i = Æ следует, что Z i+1 = Æ и т.д. Отобранные нетерминалы обладают тем свойством, что из них выводятся терминальные цепочки. Оставшиеся нетерминалы терминальных цепочек не порождают, и их можно удалить из грамматики вместе с правилами, содержащими их в левой или правой части. Этот алгоритм позволяет устранить все внешние тупики и циклические тупики внешнего типа. В рассматриваемом примере X0 = {a,c,b,q,k,m,f,d,p,r}, X1 = {C,T,B}, Z1 = {C,T,B}, X2 = {S,A,C,T,D,Q,B}, Z2 = {S,A,D,Q} X3 = {S,A,C,T,D,Q,B}, Z3 = Æ. Следовательно X3 и есть то самое множество “хороших” нетерминалов. Удалив остальные нетерминалы и все ссылки на них в правилах грамматики, мы получим грамматику: S® a A½c C½b D½k T A® c C C® k T® m D® b T B® d Q½m Q® p B½r B. Для устранения внутренних тупиков повторим процесс выбора “хороших” символов с другого конца. Положим Y0 = { S }, ... , Y i = { A | $ B® jAy, где AÎ ( VTÈ VN) и BÎ Y i-1 }, то есть Y i - множество символов (терминалов и нетерминалов), которые могут появиться в сентенциальной форме на i - том шаге вывода. В нашем примере Y0 = {S}, Y1 = {a,A,c,C,b,D,k,T}, Y2 = {c,C,k,m,b,T}, Y3 = {k,l}. Далее определим W i = Y i \ ( В нашем случае W0={S}, W1={A,C,D,T}, W2=Æ. Нетерминалы B и Q - внутренние тупики. Таким образом, грамматика без тупиков имеет вид: S® a A½c C½b D½k T A® c C C® k T® m D® b T .
Поиск по сайту: |
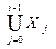 } ,
} ,
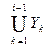 ) Ç VN, то есть новые нетерминалы, появляющиеся на i - том шаге. Очевидно, что из W i = Æ, следует что процесс можно закончить, так как все нетерминалы, выводимые из начального символа грамматики, уже получены. Остальные нетерминалы и содержащие их правила грамматики можно удалить.
) Ç VN, то есть новые нетерминалы, появляющиеся на i - том шаге. Очевидно, что из W i = Æ, следует что процесс можно закончить, так как все нетерминалы, выводимые из начального символа грамматики, уже получены. Остальные нетерминалы и содержащие их правила грамматики можно удалить.