 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Операции над КС-языками
Нетрудно показать, что целый ряд операций над КС-языками дает в результате также КС-язык. Теорема 5.4. КС-языки замкнуты относительно операций объединения, конкатенации, итерации, подстановки и обращения. Доказательство. Пусть L1=L(G1) и L2=L(G2) два контекстно - свободных языка, определяемых КС-грамматиками G1=(VT1,VN1,R1,S1) и G2=(VT2,VN2,R2,S2) соответственно. Проиндексируем нетерминалы грамматики G1 индексом 1, а нетерминалы G2 – 2 с тем, чтобы никакие имена различных грамматик не совпадали. Если объединить нетерминалы, терминалы, правила исходных грамматик и добавить к последнему объединению правило S ® S1½S2 , где S - аксиома новой результирующей грамматики, то мы, очевидно, получим КС-грамматику, определяющую объединение языков L1 и L2. Действительно, индексирование нетерминалов не изменяет класса исходных грамматик, точно так же как и объединение их правил и добавление контекстно-свободной продукции S ® S1½S2. Последняя продукция и обеспечивает порождение всех цепочек языка L1 по первой альтернативе правила и всех цепочек языка L2 по второй его альтернативе. Таким образом L= L1 È L2 = L(G), где G=( VT1ÈVT2,VN1ÈVN2,R=R1ÈR2È{S®S1|S2},S) - КС-грамматика, определяющая объединение языков L1 и L2. Точно также можно показать, что КС-грамматика G=( VT1ÈVT2,VN1ÈVN2,R=R1ÈR2È{S®S1S2},S ) определяет конкатенацию языков L1 и L2 (L(G)= L1 L2). Если к правилам P1 исходной грамматики G1 добавить правило S ® SS1½e, считая S начальным символом новой КС-грамматики G, то грамматика G будет определять итерацию языка L1 - L1* . Если же к P1 добавить правило S ® SS1½S1, или правило S ® S1S½S1, или правило S ® SS½S1, то полученная КС-грамматика G будет определять позитивную итерацию L1+. Если во всех правилах грамматики G1 вида A ® j ay заменить терминал a на S2 - аксиому грамматики G2, то полученная в результате таких преобразований КС-грамматика G будет определять не что иное, как язык L - подстановку языка L2 в язык L1 вместо терминала a:
Для того, чтобы получить грамматику, определяющую обращение LR для исходного языка L(G) достаточно обратить левые и правые части правил исходной грамматики G, то есть правила a ® b заменить на правила a R ® b R (в КС-грамматиках правила A ® b заменяются на правила A ® b R ). Такие преобразования не изменяют класса КС-грамматик и позволяют порождать все обращенные цепочки. † Все рассмотренные преобразования КС-грамматик достаточно очевидны. Рассмотрим на примере только формирование грамматики для обращения языка. Пример 5.2. Пусть задана грамматика с правилами S ® aS½bB B ® cB½d Для простоты здесь взята А-грамматика, но ничто не мешает рассматривать ее как КС-грамматику. Цепочки, порождаемые данной грамматикой состоят из необязательных символов “а” в начале цепочки, символа “b”, затем необязательных символов “c” и символа “d” в конце, т.е. цепочка имеет вид [aaa...]b[ccc...]d, где квадратные скобки традиционно обозначают необязательный элемент. Обратим правила заданной грамматики и в результате получим: S ® Sa½Bb B ® Bc½d Если правила исходной грамматики обеспечивали вывод цепочки слева направо, то полученные правила выводят ее справа налево. Цепочка, порождаемая последней грамматикой имеет вид d[ccc...]b[aaa...]. † Теорема 5.5. КС-языки не замкнуты относительно операций пересечения, допол нения и разности. Доказательство. Языки L1={a n b n c j½n ³ 1, j ³ 1} и L2={a j b nc n½n ³ 1, j ³ 1} - КС-языки. Первый из них можно определить правилами S ® XY X ® aXb½ab Y ® cY½c , а второй S ® XY X ® aX½a Y ® bYc½bc . Однако L1Ç L2= {anbncn½n ³ 1} - не КС-язык (см. следствие теоремы 5.3). Таким образом, класс КС-языков не замкнут относительно пересечения. Отсюда можно также заключить, что класс КС-языков не замкнут относительно дополнения. В силу закона де Моргана ( Для доказательства последнего положения достаточно вспомнить, что дополнение - это, по сути дела, разность множеств. †
Поиск по сайту: |
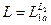 G=<VT1ÈVT2\{a},VN1ÈVN2,R=R1ÈR2È{S®aS2b}\{S1®a ab},S>
G=<VT1ÈVT2\{a},VN1ÈVN2,R=R1ÈR2È{S®aS2b}\{S1®a ab},S>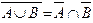 ) любой класс языков, замкнутый относительно объединения и дополнения, должен быть замкнут относительно пересечения. Из теоремы 5.4 известно, что КС-языки замкнуты относительно объединения и предположение об их замкнутости относительно дополнения приводит нас к противоречию с первым доказанным положением данной теоремы.
) любой класс языков, замкнутый относительно объединения и дополнения, должен быть замкнут относительно пересечения. Из теоремы 5.4 известно, что КС-языки замкнуты относительно объединения и предположение об их замкнутости относительно дополнения приводит нас к противоречию с первым доказанным положением данной теоремы.