 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Операции над А-языками
Теорема 5.6. Автоматные языки замкнуты относительно операций объединения, конкатенации, итерации, обращения, подстановки, пересечения, дополнения и разности. Доказательство. Проведем его конструктивно, также как и в теореме 5.4. Для представления А-грамматик используем графы состояний и в случае операций над двумя языками индексируем нетерминалы исходных грамматик. Объединение. Пусть даны два А-языка L1=L(G1) и L2=L(G2) и графы состояний грамматик G1 и G2, схематично представленные на рисунках 5.2 (а) и (б), соответственно. На рисунке 5.2 (в) представлена грамматика G, определяющая объединение исходных языков. Для ее построения вводим новый начальный символ S. Если в исходных грамматиках из S i в A i ведет ребро, помеченное терминалом a, то проведем ребро из S в A i и пометим его тем же терминалом a. Выберем новый конечный символ F и все ребра, шедшие в F1 и F2 проведем в F, а F1 и F2 удалим. Вершины S1 и S2 в общем случае удалять нельзя, так как к ним могут идти ребра, но если в S i возвратов нет, то эту вершину (нетерминал) можно удалить (в нашем примере можно удалить вершину S2 вместе с выходящими из нее дугами). Очевидно, что результирующая грамматика G является А-грамматикой. Зачастую она может быть недетерминированной, но перевод А-грамматики из недетерминированной формы в детерминированную уже был рассмотрен ранее.
Конкатенация. В этом случае получение грамматики-результата сводится к склеиванию начальной вершины S2 языка-суффикса с заключительной вершиной F1 языка-префикса, т.е. все ребра, шедшие в F1 направляются в S2 , а F1 удаляется (см. рис. 5.3 (а)).
Итерация. Для каждого ребра, идущего из некоторой вершины A исходной грамматики в заключительную вершину F, строится дублирующее его ребро, ведущее из A в начальную вершину S. На рис. 5.3 (б) добавляемые ребра выделены жирной линией.
Обращение. На рис. 5.4 (а) представлен граф исходной грамматики. Изменим имя начальной вершины S на S1 и добавим вершину S2. Для всех ребер выходящих из S1 и входящих в A добавим дуги, выходящие из S2 и входящие в A (см. рис. 5.4 (б)). Заменим имя заключительной вершины F на имя начальной - S, а имя вершины S2 на имя заключительной - F и изменим ориентацию ребер. В результате мы получим А-грамматику, определяющую обращение исходного языка. Граф этой грамматики представлен на рис. 5.4 (в). Заметим, что добавление вершины необходимо только в случае возвратов в начальную вершину исходной грамматики. Если возвратов нет, то достаточно изменить ориентацию ребер и сделать перестановку имен начального и заключительного состояний.
Подстановка. На рис 5.5 (а) представлена грамматика G2 языка L2, который мы хотим подставить вместо терминала a в язык L1 с грамматикой G1, приведенной на рис. 5.5 (б). Возьмем столько экземпляров G2, сколько в G1 имеется ребер, помеченных терминалом a. Нетерминалы в G1 отметим индексом 0, а нетерминалы в i - ом экземпляре G2 индексом i. На место каждого ребра G1, помеченного терминалом a и идущего из A0 в B0, подставим экземпляр G2, т.е. вершину A0 из G2 совместим с вершиной Si , а вершину B0 - с вершиной Fi. Отметим, что при наличии возвратов в начальную вершину грамматики G2 и других ребер, идущих из A0 грамматики G1 и помеченных терминалами, отличными от a, необходимо расщеплять начальную вершину грамматики G2 на две вершины. Одна из них в точности совпадает с исходной, а другая повторяет все выходы исходной начальной вершины, но возвраты в нее опускаются.
Именно эту, вторую начальную вершину без возвратов и совмещают с A0. Результаты этих преобразований приведены на рис. 5.5. (в), отражающем грамматику языка, полученного в результате указанной подстановки.
Пересечение. Здесь мы отойдем от принятого выше представления А-грамматик в виде графов состояний и рассмотрим построение грамматики, определяющей пересечение двух А-языков на конкретном примере. Пример 5.3. Пусть А-язык L1 определяется А-грамматикой G1= ( VT1,VN1,R1,S1) и множество R1 - это группа модифицированных правил S ® aS½bC½dC C ® bC½cC½ûëF , где F - заключительный нетерминал, и А-язык L2 определяется А-грамматикой G2=( VT2,VN2,R2,S2) и
Выполним формальную процедуру операции пересечения. Определим грамматику G=( VN , VT , R, <SR>) языка L = L1Ç L2. Для того, чтобы проконтролировать наше решение вначале определим вид цепочек, как заданных языков, так и языка - результата, благо простота выбранных грамматик позволяет легко это сделать. Цепочки языка L1 могут содержать в начале произвольное количество символов a, обязательный символ b или d, затем, возможно, серию символов b и (или) c и в завершении символ ûë. Схематично цепочку языка L1 можно представить в виде Заметим, что S Í S1Ç S2. Построение грамматики-пересечения напоминает построение детерминированной формы А-грамматики. В качестве элементов нового множества нетерминалов выбираются пары нетерминалов исходных грамматик типа <SR>, <SQ>, <SM>, <CM>, <CQ> и т.п. В результате построения правил грамматики-пересечения часть этих нетерминалов может быть исключена, как внутренние или внешние тупики. Схема построения правил новой грамматики состоит в том, что рассматриваются только те пары нетерминалов и те их альтернативы, которые имеют одни и те же терминалы в качестве продолжения цепочки. В результате мы получим грамматику <SR> ® a<SQ>½b<CM> <SQ> ® b<CQ> <CQ> ® b<CQ>½ûë<FF>. Заметим, что нетерминал <CM> не имеет общего продолжения, является внешним тупиком и его можно исключить вместе с правилом <SR> ® b<CM>. То есть операция пересечения L=L1ÇL2 определяется следующим образом: G=<VT1ÇVT2,VN={<A1A2>,A1ÎVN1,A2ÎVN2},<S1S2>,R={<AB>®a<CD>, если в исходной грамматике G1 присутствует правило вида A®aC: A,CÎVN1, B®aD, B,DÎVN2}>. В результате такого построения получается язык, включающий множество цепочек, принадлежащих языку L1 и L2. Действительно: а) если jÎL1,L2 Þ существует вывод в L1 и L2 Þ в L1: j=ab…f, значит существует вывод S1aA1bB1…fF1 в G1 и вывод в G2: S2aA2bB2…fF2.
По построению, если существуют такие правила вывода, то в L появится правило вида <S1S2>a<A1A2>…f<F1F2>. Значит, если есть такой вывод, то цепочка j принадлежит L. б) Проводя аналогичные рассуждения в обратном порядке, получим, что любая цепочка, принадлежащая языку L, принадлежит языкам L1 и L2. † Рассмотрим еще один пример:
В результате выполнения операции пересечения получим:
Поиск по сайту: |
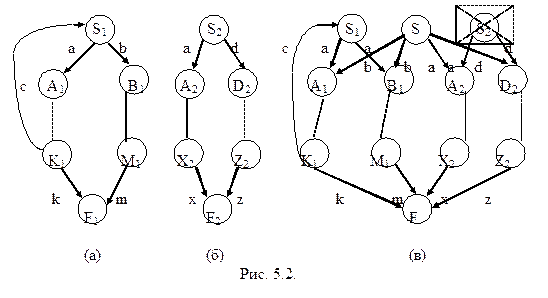




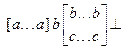 , где квадратные скобки ограничивают необязательные части строки, многоточие обозначает произвольное количество символов, а две строки - произвол в выборе символов. Цепочки языка L2 имеют вид
, где квадратные скобки ограничивают необязательные части строки, многоточие обозначает произвольное количество символов, а две строки - произвол в выборе символов. Цепочки языка L2 имеют вид 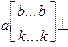 или
или  , а цепочка результирующего языка -
, а цепочка результирующего языка - 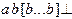 .
.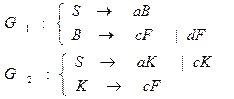

 – тупик
– тупик