 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Декомпозиция правил грамматики
Определение: две грамматики эквивалентны, если они порождают один и тот же язык. G1~G2, если L(G1)=L(G2). Теорема: не существует алгоритма, определяющего эквивалентность или неэквивалентность двух грамматик, тем не менее существуют такие преобразования исходных грамматик, которые приводят к новым грамматикам, не выходящим из класса грамматик, эквивалентных исходным. Критериями преобразования грамматик, приведения к эквивалентным грамматикам являются следующие: детерминированность; получение более короткого вывода цепочек; исключение тупиковых правил. В предыдущей главе была сформулирована теорема о существовании для любой А-грамматики эквивалентной ей грамматики во вполне детерминированной форме и доказана первая часть теоремы, подтверждающая существование таких грамматик. Ниже будет доказана вторая часть теоремы, рассматривающая эквивалентность исходной А-грамматики и построенной. Для доказательства эквивалентности исходной автоматной грамматики и построенной грамматики во вполне детерминированной форме необходимо доказать, что любая цепочка, принадлежащая языку L1, выводится и в грамматике G2 и наоборот: L1=L2, если L(G1) ÌL(G2) и L(G2) ÌL(G1).
Рассмотрим произвольную цепочку φ=a1…ak ÎL(G1), тогда существует вывод этой цепочки вида: Согласно построению, если в исходной грамматике существует правило вида S→aA1, то в преобразованной грамматике будет правило вида <S>→a<..A1…>. Аналогично рассуждаем для произвольного шага: если Ai→ai+1 Ai+1 , то <..Ai..>→ai+1<..Ai+1..> На последнем шаге вывода, имея в исходной грамматике правило вида Ak-1→akF, в преобразованной грамматике имеем правило <..Ak-1..>→ak<..F..>, то есть существует последовательность шагов вывода: <S>a1 <..A1…>..ak<..F..> => φ ÎL(G2) В противоположную сторону рассуждения абсолютно аналогичны: Пусть φ=a1…ak ÎL(G2)=> существует вывод этой цепочки в языке, порождаемом грамматикой G2, то есть существует вывод цепочки: <S>a1 <..A1…>..ak<..F..>. По построению, если существует правило вида <S>→a1<..A1…>, то в исходной грамматике существует правило вида S→a1 A1. Рассуждая аналогично, имея правило вида <..Ak-1..>→ak<..F..> в исходной грамматике, имеем правило вывода Ak-1→akF, то есть φ ÎL(G1) и => L(G2) ÌL(G1), откуда L1=L2. Что и требовалось доказать. Следующие теоремы позволяют обосновать возможность эквивалентных преобразований, приводящих к грамматикам с большим количеством правил, но вывод в которых короче. Пусть дана КС-грамматика G1=(VN,VT, R, S). Теорема 4.1. Если в КС-грамматике G1 существуют правила Y®aXb и X®g, то грамматика G2=( VN, VT,R È { Y®agb},S) эквивалентна G1. Доказательство. Проверим, что любая цепочка, выводимая в одной грамматике, выводима и в другой. Пусть j Î L(G1), тогда дерево вывода j в G1 является деревом вывода j и в G2. Обратно, пусть j Î L(G2), следовательно существует некоторое дерево вывода j в G2. Если при этом правило Y®agb не используется, то дерево вывода j в G2 является деревом вывода j в G1. Если же правило Y®agb использовалось при выводе j в G2 , то фрагмент вывода Y Þ agb заменяем на фрагмент Y Þ aXb Þ agb. В результате получим дерево, в котором используются правила только из P, то есть получим вывод цепочки в G1. Следовательно, из j Î L(G2) следует, что j Î L(G1). Теорема 4.2. Пусть в грамматике G1 имеется множество правил {Y® a Xb, X® g1 , X® g2, ... , X® gn} . Тогда, заменив это множество на множество {Y® ag1b , Y® ag2b , ... , Y® agnb , X® g1 , X® g2, ... X® gn}, получим грамматику, эквивалентную G1. И далее, если X ¹ S и других правил, которые имеют X в правой части нет, то группу правил X® g k , Доказательство. Многократно применяя теорему 4.1 в грамматику добавляем правила Y® agkb, где
Пример 4.1. Рассмотрим фрагмент грамматики для описания числа <число> ® <знак> <чбз> <знак> ® +½ -½e . Здесь в соответствии с теоремой 4.2: Y - <число>, a - пустая цепочка, X - <знак>, b - <чбз> (число без знака), g1 - +, g2 - -, g3 - e. Группу приведенных правил заменяем на правила <число> ® + <чбз>½- <чбз>½<чбз> . Теорема 4.3. Замена группы правил Y1® a 1Xb 1 , Y2® a 2Xb 2 , ... Ym® a mXbm, X® g на правила Y1® a 1gb 1 , Y2® a 2gb 2 , ... Ym® a mgb m , X® g , где других правил с нетерминалом X в левой части нет, приводит к эквивалентной грамматике. Если X ¹ S и других правил, которые имеют X в правой части нет, то правило X® g можно удалить. Доказательство здесь аналогично теореме 4.2. ƒ Пример 4.2. Замена правил: S ® AB.C½AB.½A.C½B.½.C A ® - на правила: S ® -B.C½-B.½-.C½B.½.C приводят к эквивалентной грамматике. Теорема 4.4. Декомпозиция правил. Замена в грамматике G1 группы правил При декомпозиции n+m правил грамматики заменяется на n*m правил. ƒ Пример 4.3. Рассмотрим КС - грамматику идентификатора, имеющую вид: <И> ® <Б>½<Б> <И1> <И1> ® <Б>½<Б> <И1>½<Ц>½<Ц> <И1> <Б> ® a½b½c½...½y½z <Ц> ® 0½1½2½...½8½9 В предложенной грамматике 42 правила. Проведем в ней декомпозицию по <Б> и по <Ц>. Получим новую грамматику, эквивалентную заданной. <И> ® a½...½z½a <И1>½...½ z <И1> <И1> ® a½...½z½a <И1>½...½ z <И1>½0½...½9½ 0<И1> ½...½9<И1> В результате получено 4*26=104 правил для букв и 2*10=20 правил для цифр, итого 124 правила. Правил стало больше, но вывод, а следовательно и разбор, будет короче. Нетрудно видеть, что рассмотренная декомпозиция позволила перейти от КС-грамматики идентификатора к А-грамматике. ƒ Отметим в заключении параграфа, что все рассмотренные теоремы работают в обе стороны. Так n*m правил при композиции можно заменить на n+m правил. Иногда лучше иметь правил поменьше и компактно описывать язык; иногда, с целью повышения эффективности разбора, их количество необходимо увеличить.
Поиск по сайту: |
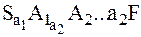
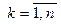 можно удалить.
можно удалить.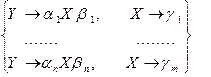 на группу правил
на группу правил  , если
, если  и других
и других  в левых и правых частях правил грамматики нет, приводит к грамматике, эквивалентной G1.
в левых и правых частях правил грамматики нет, приводит к грамматике, эквивалентной G1.