Вывод результатов и их анализ

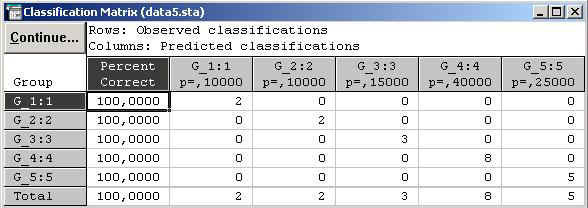
Информационная часть диалогового окна Discriminant Function Analisis Results (Результаты Анализа Дискриминантных Функций) сообщает, что:

· Number of variables in the model (число переменных в модели) =7;

· Wilks lambda (значение лямбды Уилкса) = 0,0099910;

· Approx. F(28, 33) (приближенное значение F – статистики, связанной с лямбда Уилкса) = 3,130316;

· P – уровень значимости F – критерия для значения 3,130316.

Значение статистики Уилкса лежит в интервале [0,1]. Значения статистики Уилкса, лежащие около 0, свидетельствуют о хорошей дискриминации, а значения, лежащие около 1, свидетельствуют о плохой дискриминации.

По данным показателя Wilks lambda (значение лямбды Уилкса), равного 0,00999 и по значению F – критерия равного 3,1303, можно сделать вывод, что данная классификация практически корректная.

В качестве проверки корректности обучающих выборок посмотрим результаты классификационной матрицы, нажав кнопку Classification matrix(рис. 5.7), предварительно выбрав Same for all groups в правой части окна Discriminant Function Analisis Results.

Рис. 5.7

Из классификационной матрицы можно сделать вывод, что объекты были правильно отнесены экспертным способом к выделенным группам. Но если есть предприятия, неправильно отнесенные к соответствующим группам, можно посмотреть Classification of cases (Классификация случаев) (рис. 5.8).

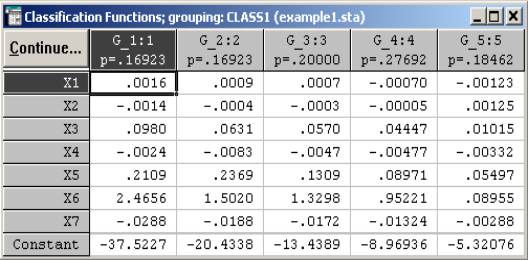
Рис. 5.8

В таблице классификации случаев некорректно отнесенные предприятия помечаются звездочкой (*). Таким образом, задача получения корректных обучающих выборок состоит в том, чтобы исключить из обучающих выборок те объекты, которые по своим показателям не соответствуют большинству предприятий, образующих однородную группу.

Для этого с помощью метрики Махаланобиса определятся расстояние от всех n объектов до центра тяжести каждой группы (вектор средних), определяемых по обучающей выборке. Отнесение экспертом i-го объекта в j-ю группу считается ошибочным, если расстояние Махаланобиса от объекта до центра его группы значительно выше, чем от него до центра других групп, а апостериорная вероятность попадания в свою группу ниже критического значения. В этом случае объект считается некорректно отнесенным и должен быть исключен из выборки.

Процедура исключения объекта из обучающих выборок состоит в том, что в таблице исходных данных у объекта, который должен быть исключен из выборки (он помечен "*"), убирается номер принадлежности к этой группе, после чего процесс тестирования повторяется. По предположению, сначала убирается тот объект, который наиболее не подходит к определенной группе, т.е. у которого наибольшее расстояние Махаланобиса и наименьшая апостериорная вероятность.

При удалении очередного объекта из группы нужно помнить, что при этом смещается центр тяжести группы (вектор средних), так как он определяется по оставшимся наблюдениям. После удаления очередного предприятия из списка обучающих выборок не исключено, что появятся новые некорректно отнесенные предприятия, которые до удаления были учтены как правильно отнесенные. Поэтому данную процедуру нужно проводить, удаляя на каждом шаге лишь по одному объекту и возвращая его обратно в обучающие выборки. Если при удаления этого объекта произошли слишком сильные изменения (большинство предприятий, которые были отнесены как правильные, помечаются как некорректно отнесенные предприятия).

Процедура исключения наблюдений продолжается до тех пор, пока общий коэффициент корректности в классификационной матрице достигнет 100%, т.е. все наблюдения обучающих выборок будут правильно отнесены к соответствующим группам.

Результаты полученных обучающих выборок, представлены в окне Discriminant Function Analisis Results (Результаты Анализа Дискриминантных Функций). В результате проведенного анализа общий коэффициент корректности обучающих выборок должен быть равен 100%.

Классификация объектов.На основе полученных обучающих выборок можно проводить повторную классификацию тех объектов, которые не попали в обучающие выборки, и любых других объектов, подлежащих группировке. Для решения данной задачи, существуют два варианта: первый – провести классификацию на основе дискриминантных функций, второй – на основе классификационных функций.

В первом случае необходимо, не закрывая диалога диалогового окна Discriminant Function Analisis Results,добавить в таблицу исходных скорректированных данных новые случаи. Для того чтобы понять, к какому классу относится этот объект, нажмите кнопку Posterior probabilities(Апостериорные вероятности). После этого вы увидите таблицу с апостериорными вероятностями. К тем группам (классам), которые будут иметь максимальные вероятности, можно отнести новые случаи.

Во втором варианте необходимо в окне диалогового окна Discriminant Function Analisis Resultsнажать кнопку Classification functions. Появится окно, из которого можно выписать классификационные функции для каждого класса (рис. 5.9). Например, для первых классов функции имеют вид:

Y₁= –37.5227+0.0016X1–0.0014X2+0.0980X3-0.0024X4+ 0.2109X5+

+2.4656X6–0.0288X7;

Y₂= –20.4338+0.0009X1-0.0004X2+0.0631X3–0.0083X4+ 0.2369X5+

+1.5020X6–0.0188X7.

Рис. 5.9

С помощью этих функций можно будет в дальнейшем классифицировать новые случаи. Новые случаи будут относиться к тому классу, для которого классифицированное значение будет максимальное. Выбор метода окончательной классификации зависит от количества новых объектов, подлежащих классификации. Если количество новых случав невелико, можно применить метод, основанный на статистических критериях. Если же количество новых случаев велико, то рациональнее по обучающим выборкам получить классификационные функции и затем, настроить формулы и провести окончательную классификацию.

Поиск по сайту: