 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Общеметодические подходы к количественной оценке риска
Риск — категория вероятностная, поэтому методы его количественной оценки базируются на ряде важнейших понятий теории вероятностей и математической статистики. Так, главными инструментами статистического метода расчета риска являются: 1) математическое ожидание m, например, такой случайной величины, как результат финансовой операции [8] k: m = Е{k}; 2) дисперсия 3) стандартное отклонение 4) коэффициент вариации Замечание. Для небольшого набора n значений – малой выборки! – дискретной случайной величины Так, средним (ожидаемым) значением выборки, или выборочным аналогом математического ожидания, является величина Аналогично, дисперсия выборки (выборочная дисперсия) определяется как среднеквадратичное отклонение в выборке:
Очевидно, что оценка стандартного (среднего квадратического) отклоненияможет быть рассчитана следующим образом Ясно, что оценка коэффициента вариации принимает теперь вид В экономических системах в условиях риска принятие решений основывается чаще всего на одном из следующих критериев. 1. Ожидаемого значения 2. Выборочной дисперсии 3. Комбинации ожидаемого значения Замечание. Под случайной величиной k в каждой конкретной ситуации понимается соответствующий этой ситуации показатель, который обычно записывается в принятых обозначениях: mp – доходность портфеля ценных бумаг, IRR – (Internal Rate of Return) внутренняя (норма) доходности [9] и т.д. Рассмотрим изложенную идею на конкретных примерах.
Поиск по сайту: |
 как характеристика степени вариации значений случайной величины k вокруг центра группирования m (напомним, что дисперсия – это математическое ожидание квадрата отклонения случайной величины от своего математического ожидания
как характеристика степени вариации значений случайной величины k вокруг центра группирования m (напомним, что дисперсия – это математическое ожидание квадрата отклонения случайной величины от своего математического ожидания  );
); ;
;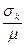 , который имеет смысл риска на единицу среднего дохода.
, который имеет смысл риска на единицу среднего дохода. речь, строго говоря, идет лишь об оценках перечисленных измерителей риска.
речь, строго говоря, идет лишь об оценках перечисленных измерителей риска.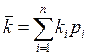 , где рi – вероятность реализации значения
, где рi – вероятность реализации значения 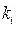 случайной величины k. Если все значения
случайной величины k. Если все значения  .
. или
или . В последнем случае выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии. Поэтому предпочтительнее использовать несмещенную оценку дисперсии
. В последнем случае выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии. Поэтому предпочтительнее использовать несмещенную оценку дисперсии  , которая задана формулой
, которая задана формулой 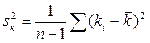 .
. или
или 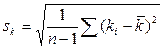 .
. .
. (доходности, прибыли или расходов).
(доходности, прибыли или расходов). или стандартного (среднего квадратического) отклонения
или стандартного (среднего квадратического) отклонения  .
.