 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формирование оптимального портфеля с помощью ведущего фактора финансового рынка.
Практика показывает, что на фондовом рынке одновременно объектом купли-продажи являются акции большого числа эмитентов, имеющие разную степень доходности. Во всех странах с развитым рынком ценных бумаг для определения общей тенденции в изменении курсов акций применяются специальные индикаторы – фондовые индексы[11] (индекс Доу-Джонса, Standard & Poors). Рыночная модель. Предположим, что доходности всех ценных бумаг за определенный период времени (например, месяц) связаны с доходностью рынка за данный период, т.е. с доходностью акции на рыночный индекс, такой, например, как индекс РТС. В этом случае с ростом рыночного индекса, вероятно, будет расти и цена акции, а с падением рыночного индекса, вероятно, будет падать и цена акции. Один из путей отражения данной взаимосвязи носит название рыночная модель (market model)[9]: mi=ai+bi´mr+ei (4.5.) где mi - доходность ценной бумаги i за определенный период (зависимая переменная); mr - доходность на рыночный индекс за этот же период (независимая, объясняющая переменная); ai - постоянная составляющая модели линейной регрессии, показывающая какая часть доходности i ценной бумаги не связана с изменением доходности на рыночный индекс, коэффициент смещения; bi - параметр линейной регрессии, называемый бета, показывающий чувствительность доходности i ценной бумаги к изменениям рыночной доходности, коэффициент наклона; ei - случайная погрешность. Оценку параметров регрессионной модели(4.5) можно получить с помощью МНК[v]. «Бета» - коэффициент Отметим, что наклон в рыночной модели ценной бумаги измеряет чувствительность ее доходности к доходности на рыночный индекс. Коэффициент наклона рыночной модели часто называют «бета»- коэффициентом (beta) и вычисляют так:
аi =
где sir- ковариация между доходностью акции i-ой бумаги и доходностью на рыночный индекс, а smr2- обозначает дисперсию доходности на индекс. Бета-коэффициент оценивает изменения в доходности отдельных акций в сопоставлении с динамикой рыночного дохода. Ценные бумаги, имеющие коэффициент выше единицы, характеризуются как агрессивные и являются более рискованными, чем рынок в целом. Бета-коэффициент может быть положительным или отрицательным. Если он положителен, то доходность соответствующих ценных бумаг будет аналогична динамике рыночной доходности. При отрицательном бета - коэффициенте эффективность данной ценной бумаги будет снижаться при возрастании эффективности рынка. Исходя из рыночной модели (4.5), общий риск ценной бумаги i, измеряемый ее дисперсией si2= Var(mi), состоит из двух частей[12]: (1) рыночный (или систематический) риск (market risk); (2) собственный (или несистематический) риск (unique risk)[vi]. Var(mi)= Var(ai+bi´mr+e)= =Var(ai)+Var(bi´mr)+Var(ei)= = Таким образом, Var(mi)= si2равняется следующему выражению: si2 = bi2smr2+se2, где
bismr обозначает рыночный риск ценной бумаги i(измеренный в СКО), а se собственный риск ценной бумаги i, мерой которого является СКО случайной погрешности ei из уравнения (4.5.).
Как отмечено выше, вариация доходности каждой ценной бумаги состоит из двух слагаемых: «собственной» вариации, не зависящей от рынка, и «рыночной» части вариации, определяемой случайным поведением рынка в целом. отношение bi2smr2/si2 обозначается Ri2и называется R-squared (в регрессионном анализе Ri2 называют коэффициентом детерминации)[vii]. Это отношение характеризует долю риска данных ценных бумаг, вносимую рынком. Те бумаги, для которых R-squared велико, в каком-то смысле предпочтительнее, так как их поведение более предсказуемо. Таким образом, коэффициент регрессии β служит количественным измерителем систематического риска, не поддающегося диверсификации. Ценная бумага, имеющая β - коэффициент, равный 1, копирует поведение рынка в целом. Если значение коэффициента выше 1, реакция ценной бумаги опережает изменение рынка как в одну, так и в другую сторону. Систематический риск такого финансового актива выше среднего. Менее рисковыми являются активы, β-коэффициенты которых ниже 1 (но выше 0). Рассмотрим в этой ситуации портфель ценных бумаг. Оказывается, доходность (рисковой части) портфеля с зафиксированными долями бумаг также линейно зависит от доходности рынка. В самом деле, пусть доля i-й ценной бумаги есть xi, тогда доходность портфеля: mp = S xi(ai + bi ´mr + e ).(4.7) Марковиц разработал очень важное положение, которое гласит: совокупный риск портфеля можно разложить на две составные части. С одной стороны, это так называемый систематический риск, который нельзя исключить, и которому подвержены все ценные бумаги практически в равной степени. С другой - специфический риск для каждой конкретной ценной бумаги, который можно избежать при помощи управления портфелем ценных бумаг. При этом сумма сложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений (например, часть средств на банковском счете вводится в модель как инвестиция с нулевым риском).
Из уравнения (4.7) можно показать, что общий риск портфеля состоит из двух компонент: рыночного риска и собственного риска. sp2 = bp2smr2+sep2 , (4.8.)
где
увеличение диверсификации (увеличение количества ценных бумаг в портфеле) приводит к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля, в то время как рыночный риск портфеля остается приблизительно таким же. Задача Марковица о формировании портфеля заданной эффективности с учетом ведущего фактора и минимального риска может быть сформулирована следующим образом [1, с.172]: Необходимо найти вектор Х= (X1, X2,… Xn), минимизирующий риск портфеля sp . sp =
Отметим основные этапы, которые необходимо выполнить для построения оптимального портфеля этой задаче: 1) Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N шагов расчета, за который будут наблюдаться значения доходности каждой ценной бумаги. 2) По рыночному индексу (например, АК&М) вычислить рыночные доходности rm для того же промежутка времени. 3) Найти ожидаемые доходности каждой ценной бумаги от рыночной доходности (от индекса рынка). 4) Определить величину дисперсии рыночного показателя smr2, а также и найти величины 5) Вычислить дисперсии 6) Подставить эти значения в соответствующие уравнения
После такой подстановки выяснится, что неизвестными величинами являются веса Хi ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля mp, можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель.
Концепция β - коэффициентов составляют основу модели оценки финансовых активов (Capital Assets Pricing Model, CAPM). При помощи этого показателя может быть рассчитана величина премии за риск, требуемой инвесторами по вложениям, имеющим систематический риск выше среднего.
Поиск по сайту: |
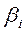 =
= 


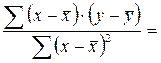
 =
=  =
=  (4.6)
(4.6)
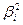 Var(mr)+ Var(ei).
Var(mr)+ Var(ei). ,
, =
=  ,
,
 ,
,




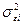 ошибок регрессионной модели
ошибок регрессионной модели