 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Бригхем Ю., Гапенски Л. Финансовый менеджмент: Полный курс: В 2-х томах / Пер. с англ. под ред. Ковалева В.В. СПб.: Экономическая школа, 1997.⇐ ПредыдущаяСтр 14 из 14
14. Галиц Л. Финансовая инженерия: инструменты и способы управления финансовым риском.—Москва:ТВП,1998.—576. с. 15. Рогов М.А. Риск-менеджмент -М.: Финансы и статистика, 2001.120 с.
[1] Так, в основе чаще всего употребляемых классификационных схем используются следующие элементы: - время возникновения; - основные факторы возникновения; - характер учета; - характер последствий; - сфера возникновения и др. Например, по времени возникновения риски распределяются на ретроспективные, текущие и перспективные. Анализ ретроспективных рисков позволяет более точно прогнозировать текущие и перспективные риски.
[2] К политическим рискам относятся: а) невозможность осуществления хозяйственной деятельности вследствие военных действий, революции, обострения внутриполитической ситуации в стране, национализации, конфискации товаров и предприятий, введения эмбарго, из-за отказа нового правительства выполнять принятые предшественниками обязательства и т. п.; б) введение отсрочки (моратория) на внешние платежи на определенный срок ввиду наступления чрезвычайных обстоятельств (забастовка, война и т. д.); в) неблагоприятное изменение налогового законодательства; г) запрет или ограничение конверсии национальной валюты в валюту платежа. В этом случае обязательство перед экспортерами может быть выполнено в национальной валюте, имеющей ограниченную сферу применения. [3] Инфляция означает обесценение денег и, соответственно, рост цен. Дефляция – это процесс, обратный инфляции, он выражается в снижении цен и, соответственно, в увеличении покупательной способности денег. [4] В теории игр аналогичные матрицы носят название матрица игры, платежная матрица, матрица выигрышей; при этом термин «выигрыш» соотносят с первым игроком (в нашем случае им является ЛПР), так что отрицательное значение такой матрицы понимается как проигрыш первого игрока. В задачах анализа финансовых операций матрица последствий называется также матрицей доходов. [5] Матрицы рисков называют также матрицами потерь, или матрицами упущенных возможностей. [6] Критерий оптимальности итальянского экономиста В.Парето применяется при решении многокритериальных задач, в которых оптимизация означает улучшение одних показателей при условии, что другие при этом не ухудшаются. [7] Множеством, или областью Парето в общем случае называют множество всех допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности в задачах многокритериальной оптимизации, т.е. невозможно улучшить хотя бы один из них, не ухудшая остальных. Принадлежащие множеству Парето решения называются эффективными, или оптимальными по Парето. [8] Под результатом финансовой операции k чаще всего понимают ее доходность (норму дохода), т.е. сумму полученных доходов, исчисленную в процентном отношении к сумме произведенных затрат. [9] Под внутренней нормой доходности (IRR) – наиболее широко используемым критерием эффективности инвестиций – понимают процентную ставку, при которой чистая современная стоимость инвестиционного проекта равна нулю. [10] Поиск решения позволяет решать задачи с нелинейными ограничениями и целевыми функциями. [11] Расчеты показателя rm производятся по акциям наиболее представительных компаний. В США чаще всего используются индексы Standard & Poors: S&P-100 (500, 1000 и др.) и индекс Доу-Джонса. Их российским аналогом можно считать сводный индекс Российской торговой системы (РТС), разработанный в 1995 г. Сегодня этот индекс де-факто является главным показателем отечественного фондового рынка, его значение по окончании торгов публикуется средствами массовой информации. Особенностью индекса РТС является большая выборка, охватывающая весь список акций категории «А» РТС (по состоянию на 20 декабря 1999 г. — 46 бумаг, 27 эмитентов). Формула, используемая для расчета индекса РТС, — взвешенное по капитализации арифметическое среднее стоимости акций компаний РТС, номинированных в долларах США. По своей сути индекс РТС отражает стоимость самых ликвидных акций российских компаний по отношению к базовой дате (1 сентября 1995 г.). Номинация стоимости акций в долларах позволяет полностью избежать влияния на оценку стоимости портфеля акций девальвационных процессов в экономике страны. С этой точки зрения индекс РТС представляется удобным для анализа иностранными портфельными инвесторами, работающими на российском рынке. Кроме индекса РТС рассчитывается значительное число индексов информационных агентств и некоторых торговых площадок, например индексы агентств АК&М, «Росбизнесконсалтинг» (РБК), «Moscow Times», ROS, а также ряд индексов фондовых бирж (в частности, ММВБ и МФБ). В большинстве своем это индексы, арифметически взвешенные по капитализации (исключение составляет индекс РБК.
[12]
[13] Подробное изложение методики работы при построении регрессионных моделей с помощью надстройки Пакет анализа можно найти в практикуме Орловой И.В. «Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL». [i] Дисперсия Дисперсия случайной величины является наиболее употребительной числовой характеристикой степени вариации значений случайной величины вокруг центра группирования. Дисперсия обычно обозначается как
Из Выборочная дисперсия
Определенная таким образом выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии. Несмещенная оценка дисперсии
[ii] Выборочная ковариация Выборочная ковариация является мерой взаимосвязи между двумя переменными. Выборочная ковариация между x и y определяется как
[iii] Коэффициент корреляции Коэффициент корреляции является более точной мерой зависимости между величинами. Подобно дисперсии и ковариации коэффициент корреляции имеет две формы – теоретическую и выборочную. Для двух переменных x и y теоретический коэффициент корреляции определяется следующим образом:
выборочный коэффициент корреляции определяется по формуле:
[iv] Риск портфеля трехфакторной модели s2p =V p = XT*COV*X [v] Оценка параметров регрессионной модели. Для оценки параметров регрессионного уравнениянаиболее часто используют метод наименьших квадратов (МНК), согласно которому в качестве оценки принимают вектор a, который минимизирует сумму квадратов отклонения наблюдаемых значений у; от модельных значений
Формула для вычисления параметров регрессионного уравнения имеет вид: a = (Xт X )-1 X т Y Рассмотрим случай зависимости переменной Y от одного фактора Х. Мы хотим подобрать уравнение
для вычисления а1 можно использовать следующие выражения: а1= а0= Вычисление параметров рыночной модели mi = ai + bi ´mf с помощью МНК:
[vi] Дисперсионный анализ модели регрессии. После построения уравнения регрессии мы можем разбить значение у, в каждом наблюдении на две составляющих - (*) Величина , — расчетное значение у в наблюдении i— это то значение, которое имел бы у при условии, что уравнение регрессии было правильным, и отсутствии случайного фактора. Это, иными словами, величина у, спрогнозированная по значению х в данном наблюдении. Тогда остаток , есть расхождение между фактическим и спрогнозированным значениями величины y. Это та часть у, которую мы не можем объяснить с помощью уравнения регрессии. Используя (*) разложим дисперсию у: (**) Это означает, что мы можем разложить Var (у) на две части: — часть, которая «объясняется» уравнением регрессии в вышеописанном смысле, и Var(e) — «необъясненную» часть. используя определение выборочной дисперсии и умножив на n обе части уравнения (**), можно представить его следующим образом: (***) где - значения y, вычисленные по модели; Se2 = =- остаточная сумма квадратов отклонений; Sy2 =- общая сумма квадратов отклонений зависимой переменной от ее среднего значения, - сумма квадратов отклонений, объясненная регрессией.
[vii] коэффициент детерминации - R2.
Он показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т. е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов. В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных. Скорректированный R2, или , рассчитывается так: , где n — число наблюдений; k — число независимых переменных.
Поиск по сайту: |
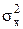 . Дисперсия – это математическое ожидание квадрата отклонения случайной величины от своего математического ожидания:
. Дисперсия – это математическое ожидание квадрата отклонения случайной величины от своего математического ожидания:
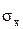 - теоретическое стандартное отклонение - стандартное отклонение случайной переменной есть квадратный корень из ее дисперсии.
- теоретическое стандартное отклонение - стандартное отклонение случайной переменной есть квадратный корень из ее дисперсии. Для выборки из n наблюдений
Для выборки из n наблюдений  выборочная дисперсия определяется как среднеквадратичное отклонение в выборке:
выборочная дисперсия определяется как среднеквадратичное отклонение в выборке: .
.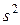 определяется по формуле:
определяется по формуле: .
.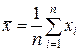
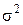
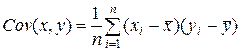
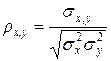 .
.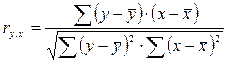
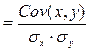 .
.

 , т. е. квадратичную форму:
, т. е. квадратичную форму: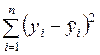 Þ min.
Þ min.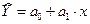 .
.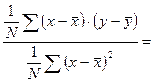

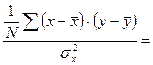
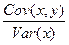 =
= 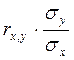

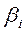 =
=  =
= 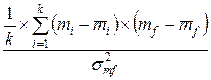
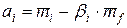
 и
и  ;
;