Пример решения и оформления типовой задачи

Таблица 3.3

Данные о стоимости ОПФ и численности работающих
на заводах отрасли народного хозяйства

По каждому признаку подсчитать итоги табл. 3.3. Построить интервальный ряд по стоимости ОПФ, предварительно сделать группировку, образовывая 5 групп заводов (с равными интервалами). Построить простой ранжированный ряд по среднесписочному числу работников за отчётный период, построить ранжированный ряд заводов по группам по стоимости ОПФ.

Решение.

Рассчитаем шаг: .

Для расчетов шага интервального ряда (нахождения максимального и минимального значений варианты), проведения итогового суммирования данных, расчетов удельного веса и других операций с данными использовать формулы для расчетов (например, расчет элементов третьей графы табл. 3.4 производится делением числа всех заводов на число заводов данной группы с предварительным определением формата ячеек этой графы как процентной), для проведения группировки, подсчёта числа заводов, средних значений результативного признака возможно применение авто фильтров с установкой условий фильтра, расчёт промежуточных итогов и применение функций Excel.

Построим интервальный ряд по стоимости ОПФ.

Таблица 3.4

Графа 3 получается в результате деления значений графы 2 на итог этой графы и задания формата ячейки как процентного (табл. 3.4).

Таблица 3.5

Ранжированный ряд по среднесписочной численности работников

Окончание табл. 3.5

Таблица 3.6

Ранжированный ряд заводов по стоимости ОПФ с разбивкой
по группам

Окончание табл. 3.6

Исходные данные. В данных таблицы имеются сведения, по которым необходимо произвести сводку и группировку так, как показано в типовой задаче. Все формулы, применяемые при составлении таблиц, указать перед таблицей (например, формулы расчета значений в графах).

Порядок оформления и защиты лабораторной работы № 8

Результаты работы оформить в виде таблиц с соответствующими формулами для их расчета. Сохранить на дискете в своем файле лист с именем лабораторная работа №3. Для защиты работы необходимо знать формулы, по которым производились расчёты.

Контрольные вопросы

1. Понятие сводки и группировки.

2. Понятие группировочного признака.

3. Что такое варьирующий признак? Приведите пример.

4. Понятие ряда распределения. Приведите пример.

5. Классификация рядов распределения.

6. Что называется вариационным рядом? Приведите пример.

7. Что называется атрибутивным рядом распределения?

8. Приведите виды вариационных рядов.

9. Что называется размахом вариации?

10. Что называется шагом или интервалом ряда?

11. Какие ряды называют интервальными, какими бывают интервальные ряды?

12. Что называется ранжированным рядом? Приведите пример.

Лабораторная работа № 9 (4 час.)

Тема: Абсолютные и относительные величины
в статистике

Цель работы

Усвоить приемы определения различных типов относительных величин и методы их расчета на основе абсолютных величин в статистике с использованием приложения Microsoft Excel.

Краткая теория

Статистические показатели в форме абсолютных величин характеризуют абсолютные размеры изучаемых статистикой процессов и явлений, отражают их временные характеристики, объем совокупности. Единицы измерения в абсолютных величинах представлены в натуральном выражении: тонны, литры, штуки, рубли и т.д. Абсолютные величины в статистике могут быть индивидуальными или суммарными, в зависимости от единиц измерения – трудовые (чел. – час., чел. – дни и т.д.), стоимостные (рубли или другие денежные единицы) или натуральные (килограммы, штуки, тонны, литры, метры и т.д.).

Относительные показатели могут быть:

· относительные показатели 1 уровня (результат от деления одного абсолютного показателя на другой абсолютный показатель);

· относительные показатели 2 и выше уровней (результат от деления одного относительного показателя на другой относительный показатель).

Все относительные показатели в статистике подразделяются на:

· динамики;

· плана;

· реализации плана;

· структуры;

· координации;

· интенсивности и уровня экономического развития;

· сравнения.

1. Относительный показатель динамики (ОПД)= Текущий показатель

__________________

Предшествующий или

базисный показатель

2. Относительный показатель плана (ОПП)=

Показатель, планируемый на (i+1)-й период

Показатель, достигнутый в i-м периоде

Относительный показатель реализации плана (ОПРП)=

Показатель, достигнутый в i-м периоде

Показатель, запланированный на i-й период

ОПП*ОПРП=ОПД

3.Относительный показатель структуры (ОПС)=

Показатель, характеризующий часть совокупности

Показатель, характеризующий совокупность в целом

4.Относительный показатель координации (ОПК)=

Показатель, характеризующий i-ю часть совокупности

Показатель, характеризующий часть совокупности, выбранную за базу сравнения

Результатом будет значение единиц структурной части, приходящихся на 1 единицу базисной.

5.Относительный показатель интенсивности (ОПИ)=

Показатель, характеризующий явление А

Показатель, характеризующий среду распространения явления А

6.Относительный показатель сравнения (ОПСр)=

Показатель, характеризующий объект А

Показатель, характеризующий объект Б

Поиск по сайту:
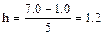