Лабораторная работа № 2

ПЕРЕЧЕНЬ ЛАБОРАТОРНЫХ РАБОТ

Лабораторная работа № 1

1 Наименование: Криптографические методы защиты информации

2 Цель работы:

Изучить криптографические методы защиты информации

3 Подготовка к занятию:

3.1 Изучить теоретические вопросы по теме

Повторить понятия криптологии

Получить допуск к работе

4 Литература:

4.1Зегжда Д.П., Ивашко А.М.Основы безопасности информационных систем – М.: Горячая линия - Телеком, - 2000. – 452с.

4.2Хорев П.Б. Методы и средства защиты информации в компьютерных системах: учеб. пособие для студ. высш. учеб. заведений – 2 изд. – М: издательский центр «Академия», 2006. – 256с.

4.3Мельников В.П., Клейменов С.А., Петраков А.М.Информационная безопасность и защита информации: Учебное пособие студ. высш. учеб. заведений. – издательский центр «Академия», 2006. – 336с. (серия «Высшее профессиональное образование»)

4.4 Партыка Т.Л., Попов И.И.Информационная безопасность: Учебное пособие для студентов учреждений среднего профессионального образования. – 2 изд., испр. и доп. М.: ФОРУМ: ИНФРА-М, 2007. – 368с. (серия Профессиональное образование).

4.5 Конспект лекций

5 Основное оборудование:

5.1 Персональный IBM PC.

6 Задание на занятие:

6.1 Зашифровать с помощью таблицы Вижинера текст требуемого варианта, приведенный в приложении 1, (номер варианта соответствует порядковому номеру студента в журнале). Таблица Вижинера приведена в приложении 2. 2.5. Зашифровать сообщение п. 2.4. усовершенствованным шифром Цезаря (приложение 3)

6.2 Зашифровать сообщение п. 2.4. с помощью тарабарской грамоты (приложение 4).

6.3 Зашифровать сообщение п. 2.4. шифром «по книге» (приложение 5).

6.4 Зашифровать текст своего варианта – ПО ПОСЛЕДНЕЙ ЦИФРЕ ПОРЯДКОВОГО НОМЕРА В ЖУРНАЛЕ шифром «по диагонали» (двумя способами), описанным в приложении 6. Использовать решетку размером 6*6. Текст разбить на блоки по 5 знаков.

6.5 Расшифровать сообщение, зашифрованное тарабарской грамотой (приложение 7).

6.6 Расшифровать сообщение, зашифрованное шифром «по книге» (приложение 8).

7 Порядок выполнения работы:

7.1 Изучить материал работы

7.2 Выполнить задание своего варианта

7.3 Ответить на контрольные вопросы

8 Содержание отчета:

8.1 Наименование и цель работы

8.2 Порядок шифрования и дешифрования данных

8.3 Ответы на контрольные вопросы

9 Контрольные вопросы:

9.1 Что такое криптология?

9.2 Виды криптографического закрытия информации

Что такое цифровая подпись?

Приложение к практическому занятию №1

Приложение 1

1. Занятия налагают отпечаток на характер

2. Дело закончено, можно расходиться

3. К невозможному никого не обязывают

4. На всю жизнь или до первой вины

5. Платон мой друг, но истина дороже

6. Следует выслушать и другую сторону

7. Звезды склоняют, но не принуждают

8. Есть у них уста, но не говорят

9. Вдвойне дает тот, кто дает скоро

10. Закон суров, но это закон

11. Карфаген должен быть разрушен

12. Никто не несет наказания за мысли

13. Я мыслю, следовательно, я существую

14. Избыток пищи мешает тонкости ума

15. ты должен, значит, можешь

16. Тот сделал полдела, кто уже начал

17. исключение подтверждает правило

18. Каждый сам находит свое счастье

19. Ничто человеческое мне не чуждо

20. Нет пророка в своем отечестве.

Приложение 2

Схема шифрования Вижинера. Таблица Вижинера представляет собой квадратную матрицу с n² элементами, где n — число символов используемого алфавита. На рис. 3.2 показана таблица Вижинера для кириллицы. Каждая строка получена циклическим сдвигом алфавита на символ. Для шифрования выбирается буквенный ключ, в соответствии с которым формируется рабочая матрица шифрования.

Осуществляется это следующим образом. Из полной таблицы выбирается первая строка и те строки, первые буквы которых соответствуют буквам ключа. Первой размешается первая строка, а под нею — строки, соответствующие буквам ключа в порядке следования этих букв в ключе. Пример такой рабочей матрицы для ключа САЛЬЕРИ приведен в средней части рис. 3.3.

Процесс шифрования осуществляется следующим образом:

1) под каждой буквой шифруемого текста записываются буквы ключа. Ключ при этом повторяется необходимое число раз; 2) каждая буква шифруемого текста заменяется по подматрице буквами, находящимися на пересечении линий, соединяющих буквы шифруемого текста в первой строке подматрицы и находящихся под ними букв ключа; 3) полученный текст может разбиваться на группы по несколько знаков. Пусть, например, Требуется зашифровать сообщение: МАКСИМАЛЬНО ДОПУСТИМОЙ ЦЕНОЙ ЯВЛЯЕТСЯ ПЯТЬСОТ РУБ. ЗА ШТУКУ. В соответствии с первым правилом записываем под буквами шифруемого текста буквы ключа. Получаем:

максимально допустимой ценой является пятьсот руб.за штуку

сальерисаль ерисальери салье рисальер исальер иса ль ериса

Дальше осуществляется непосредственное шифрование в соответствии со вторым правилом, а именно: берем первую букву шифруемого текста (М) и соответствующую ей букву ключа (С); по букве шифруемого текста (М) входим в рабочую матрицу шифрования и выбираем под ней букву, расположенную в строке, соответствующей букве ключа (С), — в нашем примере такой буквой является Э; выбранную таким образом букву помещаем в шифрованный текст. Эта процедура циклически повторяется до шифрования всего текста. На рис. 3.3 представлена схема шифрования. Эксперименты показали, что при использовании такого метода статистические характеристики исходного текста практически не проявляются в зашифрованном сообщении. Нетрудно видеть, что замена по таблице Вижинера эквивалентна простой замене с циклическим изменением алфавита, т. е. здесь мы имеем полиалфавитную подстановку, причем число используемых алфавитов определяется числом букв в слове ключа. Поэтому стойкость такой замены определяется произведением стойкости прямой замены на число используемых алфавитов, т. е. на число букв в ключе.

Расшифровка текста производится в следующей последовательности: 1) над буквами зашифрованного текста последовательно надписываются буквы ключа, причем ключ повторяется необходимое

число раз; 2) в строке подматрицы Вижинера, соответствующей букве ключа, отыскивается буква, соответствующая знаку зашифрованного текста. Находящаяся под ней буква первой строки подматрицы и будет буквой исходного текста; 3) полученный текст группируется в слова по смыслу. На рис. 3.4 данная процедура представлена в наглядном виде. Нетрудно видеть, что процедуры как прямого, так и обратного преобразований являются строго формальными, что позволяет реализовать их алгоритмически. Более того, обе процедуры легко реализуются по одному и тому же алгоритму. Одним из недостатков шифрования по таблице Вижинера является то, что при небольшой длине ключа надежность шифрования остается невысокой, а формирование длинных ключей сопряжено с трудностями.

Нецелесообразно выбирать ключ с повторяющимися буквами, так как при этом стойкость шифра не возрастает. В то же время ключ должен легко запоминаться, чтобы его можно было не записывать. Последовательность же букв, не имеющую смысла, запомнить трудно.

Приложение 3

Шифр Цезаря. Все буквы алфавита нумеруются по порядку (от 1 до 33 в русском алфавите). Затем выбирают ключ и подписывают под сообщением с повторением, например:

Операция начинается в воскресенье

Вологдав ологдаволо г давологдаво

Чтобы получить шифрованный текст, складывают номер очередной буквы с номером соответствующей буквы ключа. Если полученная сумма больше 33, то из нее вычитают 33. В результате получают последовательность чисел от 1 до 33. Вновь заменяют числа этой последовательности соответствующими буквами. Разбивают этот текст на группы единой длины (например, по 5), получают шифрованное сообщение.

Сясад ыйвэм жмтбз вюоёж пфъэф хйояд

Приложение 4

Тарабарская грамота.В этом шифре согласные буквы заменяются по схеме:

При шифровании буквы, расположенные на одной вертикали, переходят одна в другую, остальные буквы остаются без изменения.

Приложение 5

Шифр «по книге».Будем использовать стихотворение А.Н. Старикова. Текст стихотворения записывается в виде таблицы. Каждая буква сообщения шифруется парой чисел – номером строки, где встречается эта буква, и номером столбца.

Приложение 6

1. Занятия налагают отпечаток на характер

2. Дело закончено, можно расходиться

3. К невозможному никого не обязывают

4. На всю жизнь или до первой вины

5. Платон мой друг, но истина дороже

6. Следует выслушать и другую сторону

7. Звезды склоняют, но не принуждают

8. Есть у них уста, но не говорят

9. Вдвойне дает тот, кто дает скоро

10. Закон суров, но это закон

11. Карфаген должен быть разрушен

12. Никто не несет наказания за мысли

13. Я мыслю, следовательно, я существую

14. Избыток пищи мешает тонкости ума

15. ты должен, значит, можешь

16. Тот сделал полдела, кто уже начал

17. исключение подтверждает правило

18. Каждый сам находит свое счастье

19. Ничто человеческое мне не чуждо

20. Нет пророка в своем отечестве.

Приложение 7

1. О ГЁР ПЕ УФПАЮК КОЧО ПЕ ХЕСАЮК

2. ПИКГО ГЕСОЩЕГЕЛТОЕ РПЕ ПЕ ГУХЦО

3. ЭКО ЩЫСО НМЕЦОЕКОР РОИЖ ХЕСАПИЙ

4. ШУЦЕР ШЕЛЕСИКЬЛЯ НОТА РЫ РОСОЦЫ

5. НУЛЬК ЛЦЕСАЕК СУГВЕ КОК ТКО РОХЕК

6. НО ТОЛКЯР УФПАЮК СЬША НО УРАР ОЛСА

7. НО ГАЛКИ УФПАЕТ ДЕСОЕ

8. ОЩУГАЯ РЫ УГИРЛЯ ЛАРИ

9. КЫ ЦОСХЕП – ФПАГИК РОХЕВЬ.

0. ФАТОП ЛУМОШ ПО ЭКО ФАТОП

Приложение 8

1. 6,13;4,16;10,14;1,11;5,5;10,10;16,9;9,14;10,14;1,11;9,7;16,9;8,1;10,10;8,1;5,5;16,9;10,4

2. 1,1;4,2;1,18;10,12;10,14;2,2;10,4; 2,19;10,14;2,5;1,7;2,24;2,2;3,3;2,2;1,17;5,20;1,6;3,1;

1,6;2,10;13,5;1,18

3. 2,2;1,1;2,21;1,5;10,10;6,4;5,1;9,5;1,5;9,14;10,14;1,11;8,5;8,6;8,1;10,10;5,5;2,21;

1,5;10,10;7,14;9,7;16,22;2,2;8,5

4. 16,1;3,3;3,18;2,21;5,5;3,18;3,4;1,1;6,4;9,7;1,7;3,3;3,4;10,14;9,12;10,4;1,1;16,22;5,5;5,1;

3,3;2,2;9,14;16,9;3,3;1,5;1,1;5,5;1,7

5. 2,2;1,1;1,7;3,2;3,4;3,3;16,1;5,5;3,1;8,1;1,6;4,3;16,9;3,3;1,7;1,1;1,11;1,1;8,1;1,7;3,1;1,1

6. 3,2;3,4;3,3;8,1;1,7;2,21;10,14;6,4;2,2;9,14;1,2;3,1;1,1;3,4;8,5;1,7;3,1;8,1;10,10;3,15;

3,3;16,9;10,14;8,1;1,5;3,3;4,1;10,14

7. 3,3;1,5;5,5;8,1;1,7;10,12;2,2;2,3;2,21;8,1;3,3;4,16;3,3;1,2;3,1;11,15;8,1;6,4;5,5;10,10;3,3;

1,5;5,5;8,1;1,7;10,12

8. 3,3; 1,11;4,3;16,9;2,2;1,1;13,22;2,2;5,5;10,13;1,7;1,7;1,6;3,18;3,3;2,2;1,1;7,14;1,1;1,5;

3,3;10,13;1,7

9. 2,2;8,5;1,11;1,7;3,3;1,11;1,1;1,5;3,3;4,1;1,17;1,11;1,17;8,1;16,1;3,3;1,1;16,9;2,2;1,1;2,2;

1,1;1,11;10,14;7,14;2,21;3,3

0. 4,4;1,7;3,3;7,12;9,14;1,5;2,7;3,2;3,4;1,1;4,11;16,9;1,1;1,7;3,3;16,9;16,9;3,3;8,5;2,19;

7,14;1,1;1,5;5,5;2,2;8,5;1,2

Лабораторная работа № 2

1 Наименование: Криптографические методы защиты информации (система с открытым ключом)

2 Цель работы:

2.1Изучить криптографические методы защиты информации (система с открытым ключом)

3 Подготовка к занятию:

3.1 Изучить теоретические вопросы по теме

3.2 Повторить понятия криптологии

3.3 Получить допуск к работе

4 Литература:

4.1Зегжда Д.П., Ивашко А.М.Основы безопасности информационных систем – М.:Горячая линия - Телеком, - 2000. – 452с.

4.2Хорев П.Б. Методы и средства защиты информации в компьютерных системах: учеб. пособие для студ. высш. учеб. заведений – 2 изд. – М: издательский центр «Академия», 2006. – 256с.

4.3Мельников В.П., Клейменов С.А., Петраков А.М.Информационная безопасность и защита информации: Учебное пособие студ. высш. учеб. заведений. – издательский центр «Академия», 2006. – 336с. (серия «Высшее профессиональное образование»)

4.4Партыка Т.Л., Попов И.И.Информационная безопасность: Учебное пособие для студентов учреждений среднего профессионального образования. – 2 изд., испр. и доп. М.: ФОРУМ: ИНФРА-М, 2007. – 368с. (серия Профессиональное образование).

4.5 Конспект лекций

5 Основное оборудование:

5.1 Персональный IBM PC.

6 Задание на занятие:

6.1 Изучить теоретические вопросы по теме

6.2 Повторить понятия криптологии

6.3 Получить допуск к работе

7 Порядок выполнения работы:

7.1 Изучить материал работы.

7.2 Зашифровать и дешифровать сообщение, зашифрованное методом открытого ключа.

7.3 Ответить на контрольные вопросы.

8 Содержание отчета:

8.1 Наименование и цель работы

8.2 Порядок шифрования и дешифрования данных методом открытого ключа.

8.3 Ответы на контрольные вопросы

9 Контрольные вопросы:

9.1 Дайте определение ассиметричного алгоритма шифровании?

9.2 Как понимается следующая запись a = b(mod(g))?

9.3 Что такое электронная подпись?

9.4 Каков порядок шифрования при использовании электронной подписи?

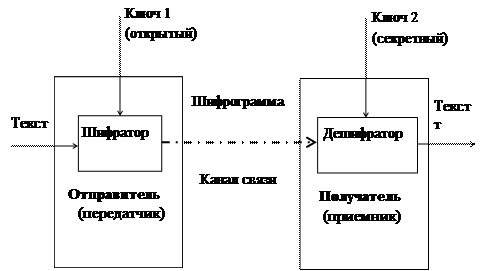
Приложение 1

Рассматриваемый метод шифрования разработали в 1976 г. американцы Уитфилд Диффи и Мартин Хеллман.

Приведем пример использования такой системы.

Пусть абонент А (например, банкир) и абонент В (например, вкладчик) решили установить между собой секретную передачу шифрованной информации с открытым ключом.

Каждый из абонентов независимо друг от друга выбирает два больших простых числа, находит их произведение, функцию Эйлера от этого произведения и выбирает случайное число, меньшее вычисленного значения функции Эйлера и взаимно простое с ним.

Напомним, что простое число — это целое положительное число, большее единицы, не имеющее других делителей, кроме самого себя и единицы. Взаимно простые числа— целые числа, не имеющие общих (простых) делителей.

Порядок создания ключей проиллюстрируем с помощью таблицы. Для наглядности числа выбраны малой величины. Фактически эти числа - 100 разрядные десятичные числа.

Использованная в таблице запись a = b(mod(g)) означает, что при целочисленном делении числа a на число g остаток равен b.

Например, 7 = 1(mod(3)). Указанную операцию легко выполнить с помощью стандартного калькулятора. Входящего в состав операционной системы MS Windows.

Функция Эйлера — арифметическая функция j(r), значение которой равно количеству положительных чисел, не превосходящих r и взаимно простых с r.

Предположим, что абонент А решил послать сообщение абоненту В. Вначале методом замены каждый символ сообщения заменяется (шифруется) числом. Допустим, что требуется переслать первую букву сообщения, которая зашифрована методом замены числом 2.

Абонент А шифрует число 2 открытым (опубликованным) ключом абонента В. Для шифрования число 2 возводится в степень s = 31, т. е.

m = 2³¹ = 2147483648.

Затем находят остаток от деления числа m на величину r = 253, в результате которого получается число 167, то есть:

2³¹ = 167 (mod(253)).

Напомним, что числа s и r являются открытым ключом абонента В.

В линию передается число 167, которое является шифром исходного числа 2.

Получив шифрограмму, абонент В использует свой секретный ключ t = 71. Для дешифрации он возводит полученное число 167 в степень 71 и находит остаток от деления на число 253. Математически это записывается так:

167⁷¹ º 2(mod(253)).

В данном случае остаток от деления равен 2, значит, шифрация и дешифрирование произошли правильно. Было передано число 2, и это же число было принято после всех преобразований.

Предположим, что абонент В решил ответить абоненту А и направить ему букву, зашифрованную числом 3.

Абонент В использует открытый (опубликованный) ключ абонента А (s = 5,r = 91) и выполняет шифрующее преобразование числа 3. Математически это записывается так:

3⁵ º 61(mod(91)).

В линию отправляется число 61. Получив это число, абонент А восстанавливает (дешифрирует) исходный текст с помощью своего секретного ключа t =29:

61²⁹ º 3(mod(91)).

В результате дешифрации на приемной стороне получено число 3, которое отправил абонент В.

Процесс передачи букв между абонентами иллюстрирует следующая таблица.

Первая строка приведенной таблицы поясняет процесс передачи буквы M от абонента А к абоненту В. Вторая строка показывает, как передается буква L от абонента В к абоненту А. В данном случае считается, что буква M кодируется числом 2, а буква L – числом 3.

В приведенных примерах был рассмотрен порядок передачи одного символа с каждой стороны. Понятно, что таким образом последовательно передается целое сообщение, но преобразование над каждым символом происходит по рассмотренной схеме. Заметим, что для использования этого метода необходимо сообщение предварительно преобразовать в набор чисел, например, с помощью кодовой таблицы.

Достоинством шифрования с открытым ключом является исключение необходимости передачи секретного ключа по закрытым каналам связи, например, с помощью курьера.

Однако у этого метода есть существенный недостаток. Используя опубликованный ключ, сообщение может прислать любой абонент, выдавая себя за другого абонента.

В подобных случаях требуется аутентификация — подтверждение авторства присланного документа. Для этих целей разработан способ шифрования, который называется электронной подписью.

Суть этого метода шифрования заключается в том, что сообщение шифруется не только опубликованным открытым ключом, но и собственным секретным ключом абонента, отправляющего сообщение.

Рассмотрим пример.

Предположим, что абонент В (вкладчик) решил послать сообщение, состоящее из числа 41, абоненту А (банкиру). Вначале вкладчик шифрует сообщение открытым ключом банкира:

41⁵ º 6(mod(91)).

В результате шифрования получено число 6.

Дальше вкладчик повторно шифрует это сообщение своим секретным ключом 71:

6⁷¹ º 94(mod(253)).

Шифрограмма 94 отправляется банкиру.

Банкир, получив секретное сообщение, использует вначале открытый ключ вкладчика:

94³¹ º 6(mod(253)).

Затем банкир использует свой секретный ключ:

6²⁹ º 41(mod(91)).

В результате абонент А (банкир) получает сообщение, состоящее из числа 41.

При использовании электронной подписи никто другой не сможет прислать банкиру сообщение (например, поручение перевести деньги) от имени абонента В, так как на передаче нужно обязательно использовать секретный ключ вкладчика, который известен только абоненту В.

Цифровая подпись используется не только для заверения текстовых или финансовых документов. Эта же информационная технология применяется для указания авторства разработанной программы. Активные элементы ActiveX, оживляющие Web-страницы, заверяются цифровой подписью. Этим повышается безопасность использования новых программных продуктов (уменьшается вероятность несанкционированной установки троянских программ).

Поиск по сайту: