 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пример: зависимость сопротивления проводника от температуры
Рассмотрим пример, где в качестве сглаживающей зависимости используется линейная функция вида y = p x + q. Пусть измеряется сопротивление некоторого металлического образца при различных значениях температуры. Результаты измерений отражены в табл. 3.
Таблица 3 Результаты измерений температуры и сопротивления
Нужно подобрать формулу R = f (t), наилучшим образом сглаживающую экспериментальную зависимость между R и t. Исходя из физических представлений зависимости сопротивления металла от температуры, можно представить искомую функцию в виде: Используя метод наименьших квадратов, найдем значения параметров:
где N = 6. Физический смысл найденных параметров очевиден: α – это изменение сопротивления при нагревании образца на 1оС; R0 – сопротивление при температуре t = 0оС. Теперь вычислим погрешность, с которой определены параметры α и R0. Применяя выражения (44), (42) и (43), соответственно получим:
В вычислениях формулы (47) сохранено более двух значащих цифр, так как погрешность ΔR не является окончательным результатом, а используется в последующих расчетах. Полученная экспериментальная зависимость сопротивления R от температуры t наилучшим образом описывается формулой
4. АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНОЙ ЗАВИСИМОСТИ ПАРАБОЛИЧЕСКОЙ ФУНКЦИЕЙ
4.1. Вычисление параметров a и b функции y = a x2 + bx Часто встречается такая зависимость между x и y, когда заведомо известно, что при x = 0 функция y = 0, но экспериментальные точки на графике «не ложатся на прямую» y = k x. В этом случае может оказаться справедливой формула y = a x2 + b x или y = a x2. Если сглаживающая функция имеет вид y = a x2 + b x, то, применяя метод наименьших квадратов, найдем общее отклонение:
Задача сводится к отысканию таких значений a и b, при которых функция S = S (a, b) минимальна, для чего необходимо решить систему:
Для упрощения записи и последующих вычислений введем обозначение:
Затем, опуская промежуточные вычисления, запишем окончательный результат:
Парабола, параметры a и b которой заданы формулами (53) и (54), наилучшим образом расположится среди экспериментальных значений.
4.2. Вычисление погрешности параметров a и b функции y = a x2 + bx Подставив производные
в формулу (5), получим формулы для расчета погрешности параметров a и b при известных Δyi:
Если значения yi измерялись однократно и их погрешности неизвестны, то, принимая во внимание формулы (6) и (7), имеем:
Теперь в формулах (56) и (57) можно вынести погрешность Δy за знак суммы. Проведя суммирование, после алгебраических преобразований получим:
4.3. Вычисление параметра c функции y = c x2и его погрешности В качестве упражнения рекомендуется самостоятельно рассчитать значения параметра c по методу наименьших квадратов для сглаживающей функции y = c x2, а также получить формулу для оценки погрешности Δc этого параметра. Проверить правильность полученных формул можно на следующем примере. Пусть измеряются координаты xi автомобиля, который движется равноускоренно из состояния покоя из начала координат, в моменты времени ti, отсчитанные от начала движения. Требуется найти ускорение, с которым двигался автомобиль. Результаты проведенных измерений приведены в табл. 4.
Таблица 4
Поиск по сайту: |
.
; (45)
(Ом), (46)
(Ом); (47)
; (48)
. (49)
. Вычисленные погрешности позволяют правильно округлить найденные значения параметров α и R0.
. (50)
или 
(51)
. (52)
; (53)
. (54)
и 
(55)
; (56)
. (57)
. (58)
; 
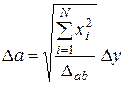. (59)