 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рассмотрим возможные значения коэффициента корреляции.
1) Величины X и Y связаны точной линейной функциональной зависимостью вида (9). Коэффициент линейной корреляции r = ±1, причем знак «плюс» или «минус» зависит от того, положителен или отрицателен коэффициент p. Сколь тщательным ни был бы эксперимент, получить r = ±1 не удастся. 2) r > 0. Между величинами X и Y существует положительная корреляция, т. е. при возрастании одной из них другая имеет тенденцию также возрастать. 3) r < 0. Между величинами X и Y существует отрицательная корреляция, т. е. при возрастании одной из них другая имеет тенденцию убывать. 4) r = 0. Величины X и Y не коррелированны, т. е. между ними не существует линейной зависимости, а точки (xi, yi) на графике не группируются около какой-либо прямой линии. Таким образом, если есть основания считать, что физические величины X и Y связаны линейной зависимостью, то можно ожидать близкое к ±1 значение коэффициента линейной корреляции r, поэтому прежде чем использовать метод наименьших квадратов для нахождения коэффициентов p и q, полезно вычислить коэффициент линейной корреляции по формулам (10) и (11).
2. АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНОЙ ЗАВИСИМОСТИ ЛИНЕЙНОЙ ФУНКЦИЕЙ ВИДА y = k x
2.1. Вычисление параметра k Наиболее простым видом функциональной зависимости является прямо пропорциональная зависимость между физическими величинами вида
В связи с тем, что значения величин x и y измеряются с погрешностью, нанесенные на координатную плоскость точки будут «разбросаны» относительно предполагаемой прямой. Необходимо отыскать такой коэффициент k (а значит, прямую, наилучшим образом согласованную с экспериментальными точками, нанесенными на плоскость (x, y)), при котором общее отклонение
Естественно, что для отыскания экстремума дифференцирование ведется по параметру, от которого зависит, как пройдет график. Воспользовавшись правилами дифференцирования суммы и сложной функции, получим
с учетом того, что xi, yi – постоянные. Раскрывая скобки и вынося параметр k за знак суммы, приходим к уравнению:
из которого находим этот параметр:
Здесь для сокращения записи и упрощения последующих расчетов введено обозначение для знаменателя
который входит во многие последующие формулы. Полученное значение параметра k позволяет наиболее близко к экспериментальным точкам провести прямую, выходящую из начала координат.
2.2. Вычисление погрешности параметра k Часто задачей эксперимента является определение коэффициента пропорциональности между двумя последовательностями чисел (например, нахождение скорости равномерного движения по измерению перемещения за разные промежутки времени). В этом случае экспериментатора интересует не только значение параметра k, но и погрешность в его определении. В соответствии с формулой (5) запишем:
Поскольку k вычисляется по формуле (18), то производная
Подставляя производную (21) в выражение (20), получим формулу для расчета погрешности параметра k:
Если погрешности Δyi не известны, положим их равными, и на основании формулы (7) с учетом зависимости (12) запишем:
Тогда, вынося в формуле (22) Δy за знак суммы и из-под квадратного корня, получим:
Окончательно запишем:
Несмотря на кажущуюся громоздкость формул (18), (19), (22) и (25), трудность вычисления можно свести к минимуму при использовании режима статистических расчетов обычных инженерных микрокалькуляторов.
Поиск по сайту: |
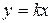 . (12)
. (12)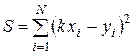 (13)
(13) Рис. 1
Рис. 1
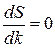 (14)
или
(14)
или
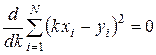 , (15)
где xi, yi – измеренные значения величин; N – количество пар значений измеренных величин.
, (15)
где xi, yi – измеренные значения величин; N – количество пар значений измеренных величин.
 (16)
(16) , (17)
, (17) . (18)
. (18) , (19)
, (19) . (20)
. (20) . (21)
. (21) . (22)
. (22) . (23)
. (23) . (24)
. (24) . (25)
. (25)