 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пример: зависимость силы тока от напряжения на резисторе
Пусть в результате измерения силы тока и напряжения на резисторе получены значения, приведенные в табл. 2.
Таблица 2 Результаты измерений силы тока и напряжения
Необходимо подобрать такую формулу U = f (I), чтобы она наиболее удачно отражала зависимость между силой тока I и напряжением U. Закон Ома устанавливает эту зависимость в виде U = R I. Это линейная зависимость. Какова же при этом величина сопротивления R? В принципе, можно определить значение R для каждого из N измерений, а именно:
а затем найти среднее значение сопротивления по формуле:
Погрешность такого косвенного измерения сопротивления можно найти по правилам обработки результатов прямых измерений, рассматривая набор значений Ri как статистический набор данных. Пренебрегая инструментальной погрешностью, получим:
Итак,
Это самый простой, но не лучший способ выбора коэффициента k в случае, когда сглаживающая зависимость между величинами X и Y линейная и имеет вид: y = k x. Применяя метод наименьших квадратов, получим
Погрешность вычислим по формуле (25) с учетом обозначения (19):
В результате получим:
Видно, что наиболее вероятные значения сопротивлений, вычисленные двумя рассмотренными способами, попадают в доверительные интервалы друг друга и, следовательно, оба имеют право на существование. Однако погрешность расчета сопротивления при использовании метода наименьших квадратов оказалась вдвое меньше по сравнению с первым способом. Таким образом, результат, полученный методом наименьших квадратов, более точен. 3. АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНОЙ ЗАВИСИМОСТИ ЛИНЕЙНОЙ ФУНКЦИЕЙ ВИДА y = p x + q
3.1. Вычисление параметров p и q Пусть в качестве сглаживающей функции y = f (x) взята линейная функция вида y = p x + q. В этом случае также можно применить метод наименьших квадратов для отыскания параметров p и q. Величина S для этого случая определяется формулой:
Необходимо выбрать числа p и q так, чтобы общее отклонение S было наименьшим. Заметим, что функция S = S (p, q) есть функция двух переменных p и q, тогда как xi, yi – постоянные величины, найденные экспериментально. Тогда для нахождения прямой, наилучшим образом согласованной с экспериментальными точками, достаточно решить систему уравнений:
После алгебраических преобразований эта система принимает вид:
Решая ее, получим искомые параметры p и q:
Здесь для сокращения записи и упрощения последующих расчетов введено обозначение для знаменателя:
который входит во все последующие формулы. Для облегчения вычислений заметим, что формулы для расчета обоих параметров содержат одни и те же суммы, а их знаменатели вообще равны. Более того, некоторые микрокалькуляторы (например, Citizen SRP-320G) имеют встроенные программы для расчета параметров p и q, что еще более облегчает процесс вычислений.
3.2. Вычисление погрешности параметров p и q Вычислим теперь погрешность параметров p и q. Полагая, что погрешностью измерения значений величины X можно пренебречь, с учетом формулы (5) запишем:
где частные производные p и q определяются следующим образом:
Подставляя производные (40) в выражения (38) и (39), получим формулы для расчета погрешности параметров p и q:
Полагая справедливым равенство (6), после алгебраических преобразований получим:
Обе формулы – (42) и (43) – содержат одни и те же суммы и тот же знаменатель, что и выражения (36). В соответствии с определением (7) погрешность Δy может быть рассчитана по формуле, аналогичной формуле (23):
Если погрешности Δyi известны, то расчет погрешностей Δp и Δq можно выполнить по формулам (41), аналогичным формуле (22).
Поиск по сайту: |
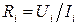 , (26)
, (26) (Ом). (27)
(Ом). (27) (Ом). (28)
(Ом). (28) Ом
Ом  . (29)
. (29) (Ом). (30)
(Ом). (30) (Ом). (31)
(Ом). (31) (Ом)
(Ом)  . (32)
. (32) . (33)
. (33)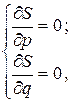 или
или  (34)
(34) (35)
(35)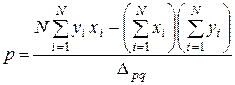 ;
;  . (36)
. (36)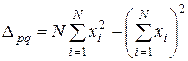 , (37)
, (37) ; (38)
; (38) , (39)
, (39) ;
;  . (40)
. (40) ;
;  . (41)
. (41) ; (42)
; (42) . (43)
. (43) . (44)
. (44)