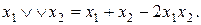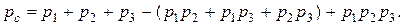|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Логико-вероятностный метод расчета надежности систем
Такое условное название получил метод расчета надежности систем, при котором математическая модель системы описывается с помощью функций алгебры логики (ФАЛ), т. е. функций, принимающих лишь два значения (y=0 или y=1) и определяемых различными наборами двоичных аргументов х1, х2, ..., xп, которые также могут находиться лишь в двух несовместных состояниях (xj=0 или xj=1). Символы х1, х2, ..., xп, характеризуют состояния элементов, причем xj=1 соответствует работоспособности элемента, xj=0 соответствует его неработоспособности. Аналогично понимают символы у=1, у=0 для системы. Функцию алгебры логики, связывающую состояния элементов с состоянием системы, называют функцией работоспособности системы. Эту функцию составляют путем анализа физических особенностей работы системы. Обычно имеют дело с монотонными ФАЛ, для которых при любых наборах Монотонными являются функции работоспособности систем, в которых замена неработоспособного элемента на работоспособный не может привести к отказу системы. От логической функции работоспособности переходят к уравнению работоспособности в символах обычной алгебры. При этом используют зависимости: если x1 и x2 связаны операцией конъюнкции, то
если x1 и x2 связаны операцией дизъюнкции, то
если x1 и x2 связаны операцией строго разделительной (исключающей) дизъюнкции («исключающее ИЛИ»), то
При использовании этих зависимостей учитывают, что x1 x1 = x1. В уравнение работоспособности вместо обозначения простых событий xj подставляют вероятности этих событий pj и вычисляют вероятность рс нахождения системы в работоспособном состоянии (в течение заданного интервала времени). Например, для системы из трех элементов, логическая схема которой изображена на рис. 10, б (нагруженное резервирование), функция работоспособности имеет вид:
где 1, 2, 3 – номера элементов. Уравнение работоспособности в символах обычной алгебры,
Выражение для вероятности безотказной работы за заданное время (0, t)
Тот же результат можно получить сразу по логической схеме для расчета надежности: Достоинства логико-вероятностного метода расчета надежности: 1) можно применять при любой логической структуре системы (не только при последовательно-параллельных логических схемах); 2) можно применять при любых распределениях наработки до отказа. Недостатки метода: 1) не всегда удается составить логическую функцию работоспособности, достаточно точно соответствующую рассматриваемой системе; 2) для сложных систем преобразования ФАЛ становятся очень громоздкими.
Поиск по сайту: |
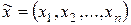 и
и  , таких, что
, таких, что  , имеет место соотношение
, имеет место соотношение  .
.