Теоретические распределения наработки до отказа

Возможны два пути вычисления показателей надежности неремонтируемых объектов по данным об отказах:

1) вычисление экспериментального распределения наработки до отказа;

2) вычисление параметров теоретического распределения наработки до отказа.

Оба пути имеют достоинства и недостатки. Исторически сложилось так, что вероятностные методы исследования в основном развиваются по пути использования теоретических распределений.

В качестве теоретических распределений наработки до отказа могут быть использованы любые применяемые в теории вероятностей непрерывные распределения. В принципе можно взять любую кривую, площадь под которой равна единице, и использовать ее в качестве кривой распределения случайной величины.

На рис. 4 приведены графики f(t) и λ(t) для четырех наиболее часто употребляемых в теории вероятностей распределений, а соответствующие функции надежности – на рис. 5.

Рис. 4. Графики λ(t) и f(t) теоретических законов распределения наработки до отказа: а – нормальное, [усеченное на интервале (0, ∞)]; б – равномерной плотности; в – показательное; г – Релея

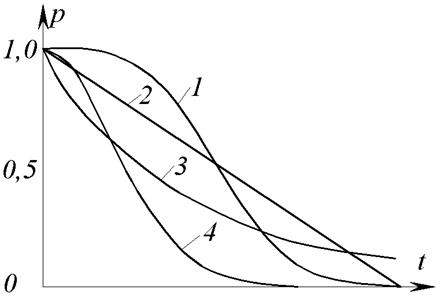
Рис. 5. Графики функций надежности. Распределения: 1 – нормальное [усеченное на интервале (0, ∞)]; 2 – равномерной плотности; 3 – показательное; 4 – Релея

Показательное (экспоненциальное) распределение

При показательном распределении наработки до отказа

λ =const; m_t = 1/λ.

Дисперсия наработки до отказа

Показательное распределение применяется чаще других при исследовании надежности изделий. Это объясняется рядом причин.

Во-первых, показательное распределение наработки до отказа типично для сложных объектов, состоящих из многих элементов с различными распределениями наработки до отказа.

Во-вторых, при постоянных интенсивностях отказов изделий получаются очень простые формулы для расчета надежности. Это связано с тем, что при λ =const вероятность безотказной работы в течение заданной наработки Δt не зависит от суммарной наработки.

В-третьих, при ограниченных экспериментальных данных трудно обнаружить значительные отклонения от гипотезы λ =const, даже если и имеется возможная нестационарность λ(t). Если экспериментальных данных недостаточно, чтобы выявить истинный характер нестационарности λ(t), принимают в качестве первого приближения λ = const.

Поиск по сайту: