 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Показатели надежности неремонтируемых объектовСтр 1 из 9Следующая ⇒
Министерство образования Российской Федерации Волгоградский государственный архитектурно-строительный университет Н.А. Михайлова, М.Ю. Нестратов, А.А. Чураков НАДЕЖНОСТЬ ТЕХНИЧЕСКИХ СИСТЕМ Утверждено редакционно-издательским советом академии в качестве учебного пособия Волгоград 2004 УДК 62-192.001.1 ББК
Михайлова Н.А., Нестратов М.Ю., Чураков А.А. Надежность технических систем и техногенный риск: Учебно-методическое пособие / ВолгГАСУ – Волгоград, 2004. – 84 с. ISBN Рассмотрены основные понятия надежности и ее составляющих (безотказности, долговечности, ремонтопригодности, сохраняемости), риска и безопасности технических систем; методы качественного анализа надежности и безопасности простых и сложных систем. Изложены вопросы предотвращения или снижения ущерба от аварийных воздействий природного и техногенного характера расчетным путем на стадии проектирования. Для студентов специальности ПБ. Ил. 22 Табл. 25 Библиогр. 11 назв.
УДК 62-192.001.1 ББК
ISBN *********** © Волгоградский государственный архитектурно строительный университет, 2004 © Михайлова Н.А., Нестратов М.Ю., Чураков А.А., 2004 Оглавление
ЧАСТЬ I ГЛАВА 1. ПОКАЗАТЕЛИ НАДЕЖНОСТИ Основные понятия теории надежности Теория надежности изучает процессы возникновения отказов технических объектов и способы борьбы с отказами. Техническими объектами могут быть изделия, системы и их элементы, в частности сооружения, установки, устройства, машины, аппараты, приборы и их части, агрегаты и отдельные детали. В последние годы область применения теории надежности расширяется, ее методы распространяются также на формализованные алгоритмы целенаправленного применения технических объектов (программы для ПК, планы систем работ) и на действия пользователя ПК как звена системы управления. Часто в целях общности речь будет идти о системах и единичных рабочих частях систем - элементах. Система предназначена для самостоятельного выполнения определенной практической задачи. Термин элементприменяется для составной части системы. Обычно элемент не предназначается для самостоятельного практического применения вне связи с другими элементами. Примеры элементов: процессор ПК. В принципе систему можно разбить на любое число элементов, необходимое для исследования (расчета) надежности. Однако деление системы на элементы нельзя считать произвольным. Каждый элемент должен обладать способностью выполнять в системе определенные функции. Иногда ставится условие, чтобы элемент был такой частью системы, которая может быть восстановлена только путем полной замены. Различают два основных состояния объектов: работоспособное и неработоспособное. Состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения заданных параметров в пределах, установленных нормативно-технической документацией, называют работоспособным. Состояние объекта, при котором значение хотя бы одного заданного параметра, характеризующего способность выполнять заданные функции, не соответствует требованиям, установленным нормативно-технической документацией, называют неработоспособным. Отказ – событие, заключающееся в нарушении работоспособности, т. е. в переходе в неработоспособное состояние. Обычно неработоспособность – состояние, при котором нельзя начинать применение объекта (например, выпускать самолет в воздух). Однако возможны задачи, в которых неработоспособность – состояние, при котором объект не может продолжать выполнять свое назначение. Возможны и другие признаки неработоспособного состояния объекта (например, объект требует среднего или капитального ремонта, производительность объекта стала ниже критической и т. д.). Поэтому при оценке надежности необходимо заранее оговорить, какое состояние объекта считается неработоспособным. Когда объект предназначен для выполнения нескольких функций, часто находят значения показателей надежности по каждой из функций. Возможен и другой путь: оценивают свойство объекта выполнять все требуемые от него функции. Отказом считается невыполнение хотя бы одной из функций независимо от того, возникла ли случайная ситуация, в которой требуется выполнение этой функции, или нет. Опишем еще одну постановку задачи оценки надежности, которая, к сожалению, довольно часто встречается в литературе. В этой задаче при оценке надежности учитывают случайную потребность в выполнении объектом отдельных функций. Пусть состоящая из п элементов система предназначена для выполнения нескольких k функций. Функционирование такой системы может быть представлено как процесс изменения вектора состояний Z(t) в пространстве состояний [x(t), y(t)], где xi – состояние i-го элемента системы, (i=1, 2, …, n; yj – переменная, характеризующая потребность в выполнении j-й функции, j=l, 2,..., k. Обычно предполагается, что отдельные координаты вектора Z(t) являются независимыми случайными функциями времени (наработки), принимающими одно из двух возможных значений:
Искомые показатели «надежности» находят как числовые характеристики некоторого функционала от случайного процесса Z(t). Понятие функционала является обобщением понятия функции. Функционал Ф определен на процессе Z(t), если каждой траектории z(t) ставится в соответствие некоторое число T=Ф[z(t)]. В рассматриваемом случае найденные показатели «надежности» характеризуют не техническую систему, а ситуацию по удовлетворению случайного спроса. Поэтому слово «надежность» приведено в кавычках. Приведенные выше соображения можно пояснить таким простейшим примером. Пусть необходимо везти груз ночью через лес, в котором могут быть грабители. Человек, охраняющий груз, вооружен пистолетом. Очевидно, что значение показателя надежности этого пистолета не должно зависеть от случайной потребности в нем, т. е. от того, нападут грабители или нет. Виды отказов объектов Отказы можно классифицировать по различным признакам. 1. По характеру устранения можно различать окончательные (устойчивые) и перемежающиеся (то возникающие, то исчезающие) отказы. Окончательные отказы являются следствием необратимых процессов в деталях и материалах. При окончательных отказах для восстановления работоспособности объекта необходимо производить его ремонт (регулировку). Пример окончательного отказа – отказ компьютера из-за выхода из строя оперативной памяти. Перемежающиеся отказы в большинстве случаев являются следствием обратимых случайных изменений режимов работы и параметров объектов. При возвращении режима работы в допустимые пределы объект сам, обычно без вмешательства человека, возвращается в работоспособное состояние. Например, совершенно исправный элемент компьютера может перестать реагировать на управляющий сигнал из-за случайного резкого уменьшения напряжения питания. Когда напряжение питания опять станет равным номинальному значению, этот элемент будет продолжать исправно работать (конечно, если в результате колебаний напряжения не произошел окончательный отказ). Обычно последствия возникновения перемежающихся отказов отличаются от последствий появления окончательных отказов. Например, если из-за низкого напряжения питания нет изображения в телевизоре, то это меньшая неприятность, чем окончательный отказ кинескопа. В ряде случаев перемежающиеся отказы дают более тяжелые последствия, чем окончательные. Перемежающиеся отказы особенно неприятны в информационных системах, где они известны под названием сбоев. Появление сбоя трудно обнаружить, так как после его исчезновения объект остается работоспособным. Таким образом, перемежающиеся отказы существенно отличаются от окончательных причиной возникновения, внешними проявлениями и последствиями проявления. Поэтому иногда целесообразно различать два показателя надежности: для окончательных отказов и для перемежающихся отказов. 2. По связи с другими отказами можно различать отказы первичные, т. е. возникшие по любым причинам, кроме действия другого отказа, и вторичные, т. е. возникшие в результате другого отказа. Например, из-за пробоя конденсатора может сгореть сопротивление. При вычислении показателей надежности обычно учитываются лишь первичные отказы. Отказы являются случайными событиями, которые могут быть независимыми или зависимыми. Отказы являются зависимыми, если при появлении одного из них изменяется вероятность появления второго отказа. Для независимых отказов вероятность появления одного из них не зависит от того, произошли другие отказы или нет.
3. По легкости обнаружения отказы могут быть очевидными (явными или скрытыми (неявными). 4. Для каждого определенного типа объектов отказы можно различать по внешним проявлениям. Например, различные отказы конденсаторов можно разбить на две группы: типа обрыв и типа замыкание. 5. По характеру возникновения можно различать отказы внезапные, состоящие в резком, практически мгновенном изменении характеристик объектов, и отказы постепенные, происходящие за счет медленного, постепенного ухудшения качества объектов. Внезапные отказы обычно проявляются в виде механических повреждений элементов (поломки, трещины, обрывы, пробои изоляции и т. п.), из-за чего эти отказы часто называют грубыми. Внезапные отказы получили свое название из-за того, что обычно отсутствуют видимые признаки их приближения, т. е. перед отказом обычно не удается обнаружить количественные изменения характеристик объекта. Постепенные отказы (параметрические, плавные) связаны с износом деталей, старением материалов и регулированием устройств. Параметры объекта могут достигать критических значений, при которых его состояние считается неудовлетворительным, т.е. происходит отказ. Внезапный отказ объекта также является следствием накопления необратимых изменений материалов. Иначе говоря, возникновение внезапного отказа также является следствием случайного процесса изменения какого-то параметра объекта. Внезапным отказ кажется лишь потому, что не контролируется изменяющийся параметр, при критическом значении которого наступает отказ объекта, обычно связанный с его механическим повреждением. Таким образом, возникновению всякого отказа предшествует накопление тех или иных изменений внутри объекта (при этом, конечно, не рассматриваются отказы, происшедшие из-за небрежности или неумения работников). Для объектов разного назначения и устройства применяются различные показатели надежности. В настоящее время можно выделить четыре группы объектов, различающиеся показателями и методами оценки надежности: 1) неремонтируемые объекты, применяемые да первого отказа; 2) ремонтируемые объекты, восстановление которых в процессе применения невозможно (невосстанавливаемые объекты); 3) ремонтируемые восстанавливаемые в процессе применения объекты, для которых недопустимы перерывы в работе; 4) ремонтируемые восстанавливаемые в процессе применения объекты, для которых допустимы кратковременные перерывы в работе. Классификация объектов по показателям и методам оценки надежности приведена на рис.1, где прямоугольниками выделены перечисленные выше группы объектов.
Рис. 1. Группы объектов, различающиеся показателями надежности. Показатели надежности неремонтируемых объектов Такие объекты работают, до первого отказа. Для оценки надежности неремонтируемых объектов используют вероятностные характеристики случайной величины – наработки до отказа T. Под наработкой понимают продолжительность или объем работы объекта, измеряемые в часах, километрах, гектарах, циклах, кубометрах или в других единицах. Когда наработку выражают в единицах времени, иногда используют термин «время безотказной работы», или, что то же самое, «время до появления отказа». Полной характеристикой любой случайной величины является ее закон распределения, т. е. соотношение между возможными значениями случайной величины и соответствующими этим значениям вероятностями. Распределение наработки до отказа может быть описано с помощью различных показателей надежности неремонтируемых изделий. К числу таких показателей относятся: · функция надежности р(t); · плотность распределения наработки до отказа f(t); · интенсивность отказов λ(t). Функцией надежности называют функцию, выражающую вероятность того, что Т – случайная наработка до отказа объектов - будет больше заданной наработки (0, t), отсчитываемой от начала эксплуатации, т. е. p(t) =P (T ≥t). Перечислим некоторые очевидные свойства р(t): 1) р(0) =1, т. е. можно рассматривать безотказную работу лишь тех объектов, которые были работоспособны в момент включения; 2) p(t) является монотонно убывающей функцией заданной наработки t; 3) p(t) → 0 при t → ∞ т. е. любой объект со временем откажет. Наряду с p(t) используется и функция ненадежности: q(t)=1–p(t)=P{T<t}. Она характеризует вероятность отказа объекта на интервале (0, t). Функция ненадежности является функцией распределения случайной величины T; Эта функция иногда обозначается F(t). На рис. 2 приведены графики одной из возможных функций надежности p(t) и соответствующей функции q(t).
Рис 1.2. Функции надежности p(t) и ненадежности q(t) объекта. Во многих задачах в качестве показателя надежности используется вероятность безотказной работы – вероятность того, что в пределах заданной наработки не возникает отказа объекта. При этом обычно имеют в виду условную вероятность p(t1, t2) безотказной работы в течение наработки от t1 до t2 при условии, что в момент времени t1 объект был работоспособным. Эту условную вероятность можно определить по функции надежности. Рассмотрим два интервала (0, t1) и (t1, t2). Событие, состоящее в безотказной работе в течение интервала (0, t2) является совмещением двух событий: 1) объект безотказно работал на интервале (0, t1); 2) оставшийся работоспособным к моменту t1 объект безотказно проработал на интервале (t1, t2). Поэтому согласно правилу умножения вероятностей p(t2) = p(t1) p(t1, t2) следовательно
Таким образом, условная вероятность безотказной работы на интервале (t1, t2) равна отношению значений функции надежности в конце и в начале интервала. Надежность малых неремонтируемых объектов не всегда удобно характеризовать вероятностью безотказной работы, так как для небольших периодов заданной наработки значения p(t1, t2) будут близкими к единице. Поэтому наряду с р(t) используются и другие показатели надежности, например плотность распределения наработки до отказа
Плотность распределения наработки до отказа f(t) является дифференциальной формой закона распределения наработки до отказа. Плотность f(t) является неотрицательной функцией, причем
График f(t) часто называют «кривая распределения наработки до отказа». В соответствия с (2) функция надежности и функция ненадежности связаны с f(t) соотношениями
Величина f(t)dt характеризует вероятность отказа за интервал наработки (t, t+dt) объекта, взятого наугад из множества одинаковых объектов. При этом неизвестно, работоспособен ли, этот объект к началу интервала (т. е. в момент t) или отказал ранее. Это не всегда удобно на практике, и f(t) как самостоятельный показатель надежности неремонтируемых объектов находит ограниченное применение. Чаще применяют интенсивность отказовλ(t) – условную плотность вероятности возникновения отказа неремонтируемого объекта, определяемую для рассматриваемой наработки при условии, что до этой наработки отказ не возник. Интенсивность отказов можно рассматривать как относительную скорость уменьшения значений функции надёжности с увеличением интервала (0, t). Чтобы пояснить смысл этой характеристики, проведем следующие рассуждения. Введем хорошо согласующееся с практикой предположение о том, что вероятность o(t) появления двух и более отказов за бесконечно малый интервал наработки (t, t+dt)убывает быстрее, чем длина этого интервала, т. е. o(t) является бесконечно малой более высокого порядка, чем dt. Иными словами, если имеется группа одинаковых объектов,товероятность того, что в одно и тоже мгновение откажет сразу несколько одинаковых объектов очень мала. Таким образом, из рассмотрения исключаются такие явления, как катастрофы и стихийные бедствия. Рассмотрим два смежных интервала наработки (0, t) и (t, t+dt). Для того чтобы некоторый объект имел возможность отказать в интервале наработки (t, t+dt), он должен безотказно работать в течение (0, t). Согласно правилу умножения вероятностей вероятность отказа объекта в течение наработки (t, t+dt) q (t, t+dt) = f(t)dt=p(t)z, (3) где p(t) – вероятность безотказной работы объекта в течение наработки (0, t), т. е. значение функции надежности; z – условная вероятность отказа объекта за малую наработку (t, t+dt), найденная в предположении, что он безотказно проработал интервал (0, t). Условную вероятность отказа объекта в течение наработки(t, t+dt) в предположении его безотказной работы до момента t обычно выражают формулой z=λ(t)dt, где величина λ(t)называется интенсивностью отказов. Таким образом, при использовании λ(t)рассматривается лишь остающиеся работоспособными к моменту объекты, отказавшие исключаются из рассмотрения. Из (2) и (3) получаем:
Решение уравнения (4) при начальном условии р(0) = 1 дает для функции надежности формулу
При λ = const формула (5) существенно упрощается:
Вероятность безотказной работы в течение наработки (t1, t2) объекта, который был работоспособным к началу этого интервала,
При λ =const вероятность безотказной работы в течение наработки (t1, t2) не зависит от возраста объекта:
где t'=t2 –t1. При λt'<< 1обычно полагают:
В качестве показателей надежности неремонтируемых объектов применяют также числовые характеристики случайной наработки до отказа. Их обычно легче определить по экспериментальным данным, чем p(t), λ(t), f(t). Наиболее часто используют среднюю наработку до отказа (математическое ожидание наработки до отказа). Согласно определению математического ожидания непрерывной неотрицательной случайной величины
где F (t) – функция распределения случайной величины Т. Интегрируя по частям, получаем:
Первое слагаемое в этом равенстве
Это можно пояснить следующими рассуждениями. Если неотрицательная случайная величина Т имеет конечное математическое ожидание, т. е. интеграл Так как
то при у→ ∞
Следовательно
и средняя наработка до отказа
Таким образом, средняя наработка до отказа численно равна площади под кривой p(t). При λ =const имеем
Подставив в (6) значение t=mt =1/λ, получим, что при λ = const среднюю наработку до отказа можно понимать как наработку t = mt, в течение которой объект остается работоспособным с вероятностью р(t=mt)=ехр(-1)≈0,37. Для малых неремонтируемых объектов, например элементов интегральных микросхем, средняя наработка до первого отказа является понятием условным, так как обычно они не эксплуатируются столь долго и устаревают гораздо раньше, чем успевают наработать mt . Значения mt обычно вычисляются по экспериментальным данным об отказах элементов в начальный период их эксплуатации. Поэтому mt можно понимать как среднюю наработку до отказа, которая имела бы место в действительности, если бы элемент сохранял в течение всего периода использования ту интенсивность отказов, которой он обладал в начальный период эксплуатации или на испытаниях. На практике представляют интерес две условные средние наработки неремонтируемых объектов: 1) средняя полезная наработка 2) средняя продолжительность предстоящей работы При вычислении средней полезной наработки Согласно определению математического ожидания имеем:
Интегрируя по частям, получаем:
При вычислении условной средней продолжительности предстоящей безотказной работы имеем:
где
поэтому
Подставляя (12) в (11) и интегрируя по частям, получаем:
Учитывая (9), (10) и (13), получаем соотношение между средними наработками Это соотношение иллюстрирует рис. 1. 3. При λ =const имеем:
Рис. 3. К вопросу о вычислении условных средних наработок. а) – полезная средняя наработка При оценке параметрической, т. е. по постепенным отказам, надежности целесообразно учитывать стратегию замен рассматриваемых объектов. Если производятся индивидуальные замены, т. е. каждый конкретный объект из множества одинаковых эксплуатируется до отказа, то используют рассмотренные выше показатели надежности. При второй стратегии (групповые замены) эксплуатация всех объектов данного типа прекращается при достижении назначенного ресурса (заданной суммарной наработки). В течение назначенного ресурса должны практически отсутствовать параметрические отказы из-за старения, изнашивания и других причин. Иначе говоря, назначенный ресурс должен быть меньше наработки tн до начала массовых параметрических отказов. Возможны различные определения tн. Наиболее общее состоит в том, что величина tн равна суммарной наработке от начала эксплуатации, при которой плотность распределения f(t) ≈ λ(t) впервые достигает критического значения fкр≈λкр. При этом неявно учитывается известный из опыта эксплуатации факт: для параметрических отказов из-за старения, изнашивания и других нестационарных процессов при t=0 всегда f(0) =λ(0) = 0. Так как распределение наработки до появления параметрического отказа обычно является унимодальным, то величину fкр≈λкр удобно задавать в долях от моды f(tМ), например fкр=0,01f(tМ). Другие определения tн основаны на рассмотрении особенностей левой ветви теоретического распределения наработки до параметрического отказа. Здесь величина tн уже не связана с достижением определенного значения fкр≈λкр.
Поиск по сайту: |

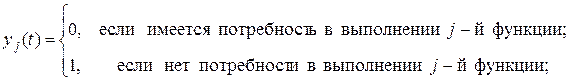



 (1)
(1) (2)
(2)
 ;
;
 .
. (4)
(4) (5)
(5) (6)
(6) (7)
(7)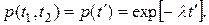 (8)
(8)

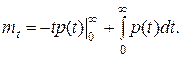

 cxoдится, то интеграл
cxoдится, то интеграл  при у→ ∞.
при у→ ∞.
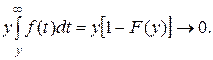
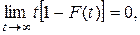
 (9)
(9)
 при условии, что при достижении наработки t1 все оставшиеся работоспособными объекты снимаются с эксплуатации;
при условии, что при достижении наработки t1 все оставшиеся работоспособными объекты снимаются с эксплуатации; при условии, что объект безотказно работал на интервале (0, t1).
при условии, что объект безотказно работал на интервале (0, t1).
 (10)
(10) (11)
(11)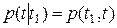 – условная вероятность безотказной работы в течение наработки (t1, t) при условии, что в момент времени t1 объект работоспособен. В соответствии с (1)
– условная вероятность безотказной работы в течение наработки (t1, t) при условии, что в момент времени t1 объект работоспособен. В соответствии с (1)
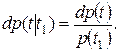 (12)
(12) (13)
(13) (14)
(14)


 ; б) – средняя продолжительность предстоящей безотказной работы
; б) – средняя продолжительность предстоящей безотказной работы 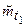 .
.