 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЗАДАЧА З ТЕОРІЇ МАРКОВСЬКИХ ЛАНЦЮГІВ ⇐ ПредыдущаяСтр 5 из 5
З НЕПЕРЕРВНИМ ЧАСОМ
Б.3.1 Постановка задачі Розглядається процес роботі ЕОМ. Потік відмов (збоїв) працюючої ЕОМ – найпростіший з інтенсивністю Знайти: 1) ймовірність того, що у момент часу 2) ймовірність того, що за час 3) фінальні ймовірності станів ЕОМ.
Б.3.2 Розв'язання задачі 1) Стани системи
Рис. Б.3.1 По графу станів, див. мал. Б.3.1, і формулі (Б.2.3) складаємо систему диференціальних рівнянь Колмогорова для ймовірністей станів
З двох рівнянь системи (Б.3.1) одне (будь-яке) може бути відкинуте, оскільки для будь-якого моменту
Розв’язуємо одержане рівняння:
У початковий момент часу ЕОМ справна. Тому рівняння (Б.3.2) розв’язуємо за початкової умови
Остаточно маємо, що:
звідки
2) Для знаходження ймовірності
Рис. Б.3.2 Стан
Розв’язуємо рівняння за початкової умови
звідки
Отже, ймовірність того, що за час
3) Фінальні ймовірності станів ЕОМ, відповідно до розділу Б.2, можна одержати, розв’язавши систему (Б.3.1), якщо покласти в ній:
Враховуючи, що
звідси
Тоді
Отже, фінальні ймовірності станів ЕОМ:
ВИСНОВОК У даній курсовій роботі обчислені ймовірності станів ЕОМ, а також її фінальні ймовірності. ЕОМ переходить із стану в стан під дією найпростіших потоків подій. Тому процеси, що відбуваються в системі (ЕОМ) розглядаються як марківські ланцюги з неперервним часом. Для того, щоб знайти ймовірності станів системи, був побудований розмічений граф станів системи. Виходячи з графа станів, одержана система диференціальних рівнянь Колмогорова, розв’язок якої дозволив знайти шукану ймовірність. Певні труднощі виникли, коли обчислювалася ймовірність того, що за час Фінальні ймовірності, в нашій роботі, також обчислювалися за допомогою системи диференціальних рівнянь Колмогорова. Проте можна було б діяти інакше: обчислити границю (Б.2.6) від ймовірностей станів (Б.3.3) і (Б.3.4). Значення кожної фінальної ймовірності дозволяє судити про середній відносний час перебування системи в даному стані. Це є вельми важливим чинником для прогнозування роботи системи. Методи, розглянуті в роботі, можна використовувати при розв’язанні деяких економічних задач, в системах масового обслуговування, в задачах прогнозування і т. ін. СПИСОК ЛІТЕРАТУРИ 1. Вентцель Е.С. Теория вероятностей: Учебник для вузов. – 5-е изд. стер. – М.: Высшая школа, 1998. – 576 с. 2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. – Изд. 6-е. стер. – М.: Высшая школа, 1998. – 479 с. 3. Тевяшев А.Д. Теория вероятностей и математическая статистика: Учебное пособие. – Харьков ХНУРЕ, 2002. – 572 с. Методичні вказівки щодо виконання курсових робіт з навчальної дисципліни "Випадкові процеси" для студентів ІІІ курсу денної форми навчання зі спеціальності 6.080200 – "Інформатика" (у тому числі скорочений термін навчання)
Укладачі: старш. викл. О.Г. Галаган, старш. викл. А.І. Галаган Відповідальний за випуск зав. кафедри ІВМ В.П. Ляшенко
Підп. до др. ______________. Формат 60х84 1/16. Папір тип. Друк ризографія. Ум. друк. арк. ____. Наклад _______ прим. Зам. №___________. Безкоштовно.
Видавничий відділ КДПУ
Поиск по сайту: |
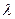 . Якщо ЕОМ дає збій, то він негайно виявляється, і обслуговуючий персонал приступає до ремонту. Закон розподілу часу ремонту – показниковий з параметром
. Якщо ЕОМ дає збій, то він негайно виявляється, і обслуговуючий персонал приступає до ремонту. Закон розподілу часу ремонту – показниковий з параметром 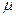 :
: 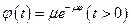 . У початковий момент часу
. У початковий момент часу 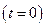 ЕОМ справна.
ЕОМ справна.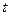 ЕОМ працюватиме;
ЕОМ працюватиме;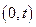 ЕОМ дасть хоча б один збій;
ЕОМ дасть хоча б один збій;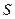 (ЕОМ) наступні:
(ЕОМ) наступні: 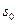 – система справна, працює;
– система справна, працює; 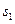 – система несправна, ремонтується. Розмічений граф станів даний на рис. Б.3.1.
– система несправна, ремонтується. Розмічений граф станів даний на рис. Б.3.1.
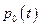 і
і 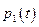
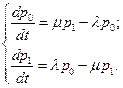 (Б.3.1)
(Б.3.1)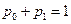 . Підставляючи в перше з рівнянь системи (Б.3.1)
. Підставляючи в перше з рівнянь системи (Б.3.1) 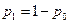 , одержуємо одне диференціальне рівняння відносно
, одержуємо одне диференціальне рівняння відносно 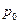 :
: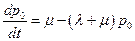 . (Б.3.2)
. (Б.3.2)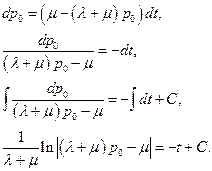
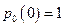 , одержимо:
, одержимо: ,
, .
. , (Б.3.3)
, (Б.3.3) . (Б.3.4)
. (Б.3.4)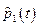 того, що за
того, що за  – ЕОМ жодного разу не давала збою;
– ЕОМ жодного разу не давала збою; 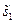 – ЕОМ хоча б один раз дала збій. На рисунку Б.3.2 даний розмічений граф станів цієї системи.
– ЕОМ хоча б один раз дала збій. На рисунку Б.3.2 даний розмічений граф станів цієї системи.
 .
. (оскільки в початковий момент система знаходиться у стані
(оскільки в початковий момент система знаходиться у стані  ,
, .
.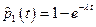
 . Маємо систему лінійних алгебраїчних рівнянь:
. Маємо систему лінійних алгебраїчних рівнянь: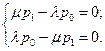 (Б.3.5)
(Б.3.5) ,
,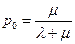 .
.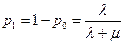 .
.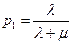 .
.