 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРИБЛИЗНИЙ ПЕРЕЛІК ТЕМ КУРСОВИХ РОБІТ
ТА ВИМОГИ ДО НИХ
1. Задачі кореляційної теорії випадкових процесів та методи їх розв'язування. До теоретичної частини необхідно включити основні положення кореляційної теорії випадкових процесів, формули та теореми, які використовують при розв’язуванні задачі, аналіз методів кореляційної теорії випадкових процесів. Задача визначається керівником. 2. Розв’язування задач теорії стаціонарних випадкових процесів. Початкові дані у більшості випадків відповідають задачам аналізу характеристик стаціонарного випадкового процесу після їх перетворення стаціонарною лінійною динамічною системою. Теоретична частина повинна містити основні положення теорії стаціонарних випадкових процесів, формули та теореми, які використовують при розв’язуванні задачі, аналіз методів теорії стаціонарних випадкових процесів. Задача визначається керівником. 3. Задачі теорії марковських ланцюгів з дискретним часом та методи їх розв’язування. Розглянути елементи теорії марковських ланцюгів з дискретним часом та методи розв’язування задач. Зробити аналіз можливості використання розглянутих методів для індивідуальної курсової роботи. Задача визначається керівником. 4. Розв’язування задач теорії марковських ланцюгів з неперервним часом. В теоретичній частині розглянути елементи теорії марковських ланцюгів з неперервним часом, зробити аналіз методів розв’язування відповідних задач. Розв’язати поставлену задачу згідно з обраним методом. Задача визначається керівником. 5. Задачі теорії систем масового обслуговування та методи їх розв’язування. Дати основні поняття теорії систем масового обслуговування. Розглянути теоретичний матеріал якій використовується для аналізу та розв’язування відповідної задачі. Розв’язати визначену керівником задачу з урахуванням методів теорії систем масового обслуговування.
ЗРАЗОК ВИКОНАННЯ КУРСОВОЇ РОБОТИ У додатку Б міститься зразок курсової роботи по дисципліні «Випадкові процеси». Він написаний згідно з вимогами даних «Методичних матеріалів» і може бути використаний студентами як наочний посібник з оформлення курсових робіт. Тема, розглянута в «Зразку» повністю відповідає переліку тем по дисципліні «Випадкові процеси». У зв'язку з цим його можна використовувати як методичні вказівки для самостійної роботи студентів. Теоретичний матеріал основної частини (розділ Б.1, розділ Б.2) викладений в скороченому (схематичному) вигляді. Виконуючи курсову роботу, студент повинен доповнити основну частину формулюваннями і доказами властивостей, теорем, якими він користувався при рішенні задачі. Можна наводити приклади, ілюстрації які сприяють розкриттю теми. Додаток А Зразок титульної сторінки МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ КРЕМЕНЧУЦЬКИЙ ДЕРЖАВНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ
Кафедра "Інформатика і вища математика"
ПОЯСНЮВАЛЬНА ЗАПИСКА
до курсової роботи з навчальної дисципліни
"ВИПАДКОВІ ПРОЦЕСИ"
Тема "____________________________________"
Виконав студент групи_________ _____________________________ П.І.Б.
Керівник_____________________ П.І.Б.
Кременчук 2006 Додаток Б Зразок курсової роботи з дисципліни "Випадкові процеси" МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ КРЕМЕНЧУЦЬКИЙ ДЕРЖАВНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ
Кафедра "Інформатика і вища математика"
ПОЯСНЮВАЛЬНА ЗАПИСКА
до курсової роботи з навчальної дисципліни
"ВИПАДКОВІ ПРОЦЕСИ"
Тема "Розв’язування задач теорії марківських ланцюгів з неперервним часом"
Виконав студент групи І-04-1 Петренко Сергій Михайлович П.І.Б.
Керівник Векшин Іван Іванович П.І.Б.
Кременчук 2006 РЕФЕРАТ
У роботі: 14 сторінок, 2 малюнки, 3 літературних джерела. Метою роботи є поглиблення теоретичних знань та придбання практичних навиків у розв’язуванні задач з теорії марківських ланцюгів з неперервним часом. Результат роботи – розв’язок задачі з аналізу системи. Процеси, що переводять систему із одного стану в інший, є марківськими ланцюгами з неперервним часом. Виходячи з цього, одержані ймовірності станів і фінальні ймовірності системи. МАРКІВСЬКИЙ ЛАНЦЮГ З НЕПЕРЕРВНИМ ЧАСОМ, НАЙПРОСТІШИЙ ПОТІК ПОДІЙ, ПОКАЗНИКОВИЙ РОЗПОДІЛ, ЙМОВІРНОСТІ СТАНІВ, ФІНАЛЬНА ЙМОВІРНІСТЬ, СИСТЕМА ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ КОЛМОГОРОВА. ЗМІСТ Завдання............................................................................................................. 4 Вступ.................................................................................................................. 5 Розділ Б.1 Потоки подій.................................................................................... 6 Розділ Б.2 Марківськи ланцюги з неперервним часом.................................... 7 Розділ Б.3 Задача з теорії марківських ланцюгів з неперервним часом...... ..9 Б.3.1 Постановка задачі........................................................................... 9 Б.3.2 Розв'язання задачі........................................................................... 9 Висновок.......................................................................................................... 13 Список літератури........................................................................................... 14 ВСТУП
В даний час широке застосування в різних напрямах науки, техніки, народного господарства одержали так звані марківські процеси. Аналіз роботи систем стан яких змінюється випадковим чином в довільний момент часу, за певних умов, можливо зводити до аналізу марківських ланцюгів з неперервним часом. Дана курсова робота присвячена аналізу системи (ЕОМ), час ремонту, для якої, розподілено по показниковому закону. Потік відмов ЕОМ – найпростіший. Це дозволяє, для дослідження роботи ЕОМ, використовувати марківські ланцюги з неперервним часом. Для виконання курсової роботи необхідно освоїти методику рішення відповідних задач, закріпити і поглибити знання пов'язані з теорією марківських процесів. Що відкриває широкі можливості для вирішення подібних і більш складних задач. РОЗДІЛ Б.1 ПОТОКИ ПОДІЙ
Потоком подій називається послідовність однорідних подій, що з'являються одне за іншим у випадкові моменти часу. Потік подій називається стаціонарним, якщо його імовірнісні характеристики не залежать від вибору початку відліку. Потік подій називається ординарним, якщо ймовірність попадання на елементарний інтервал часу Потік подій називається потоком без наслідку, якщо число подій, що потрапляють на будь-який інтервал часу Потік подій називається найпростішим, якщо він стаціонарний, ординарний і не має наслідку. Інтервал часу
де Інтенсивністю РОЗДІЛ Б.2
Поиск по сайту: |
 двох і більше подій істотно менша за ймовірність попадання на цей проміжок однієї події.
двох і більше подій істотно менша за ймовірність попадання на цей проміжок однієї події. , не залежить від того, скільки подій потрапило на будь-який інший непересічний з ним інтервал.
, не залежить від того, скільки подій потрапило на будь-який інший непересічний з ним інтервал. між двома сусідніми подіями найпростішого потоку має показниковий розподіл
між двома сусідніми подіями найпростішого потоку має показниковий розподіл (при
(при 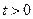 ), (Б.1.1)
), (Б.1.1)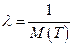 – величина зворотна середньому значенню інтервалу
– величина зворотна середньому значенню інтервалу 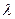 потоку подій називається середнє число (математичне очікування числа) подій, що доводяться на одиницю часу. Для стаціонарного потоку
потоку подій називається середнє число (математичне очікування числа) подій, що доводяться на одиницю часу. Для стаціонарного потоку 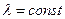 ; для нестаціонарного потоку інтенсивність, в загальному випадку, залежить від часу:
; для нестаціонарного потоку інтенсивність, в загальному випадку, залежить від часу:  .
.