 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МАРКІВСЬКІ ЛАНЦЮГИ З НЕПЕРЕРВНИМ ЧАСОМ
Функція Реалізацією випадкової функції Випадкову функцію Випадковий процес, що протікає в деякій фізичній системі Марківський випадковий процес з дискретними станами і неперервним часом називають неперервним марківським ланцюгом. Щільністю ймовірності переходу При розгляді випадкових процесів з дискретними станами і неперервним часом зручно представляти переходи системи Нехай система
де - Очевидно, що для будь-якого
Для знаходження ймовірності (Б.2.1) потрібно розв’язати систему диференціальних рівнянь (рівнянь Колмогорова), що мають вигляд:
Інтенсивності Щоб розв’язати систему (Б.2.2) для ймовірностей станів
сума яких дорівнює одиниці:
Якщо всі потоки подій, що переводять систему із стану в стан, є найпростішими, в деяких випадках існує фінальні (або граничні) ймовірності станів
не залежні від того, в якому стані система Система, в якій існує фінальні ймовірності, називається ергодичною і відповідний випадковий процес - ергодичним. Фінальні ймовірності станів (якщо вони існують) можна знайти розв’язавши систему лінійних алгебраїчних рівнянь; систему отримують з диференціальних рівнянь Колмогорова, поклавши їх ліві частини (похідні) такими що дорівнюють нулю. РОЗДІЛ Б.3
Поиск по сайту: |
 називається випадковою функцією, якщо її значення при будь-якому аргументі
називається випадковою функцією, якщо її значення при будь-якому аргументі 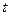 є випадковою величиною.
є випадковою величиною.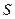 , називається марківським (або процесом без наслідку), якщо він має наступну властивість: для будь-якого моменту часу
, називається марківським (або процесом без наслідку), якщо він має наступну властивість: для будь-якого моменту часу  ймовірність будь-якого стану системи в майбутньому (при
ймовірність будь-якого стану системи в майбутньому (при  ) залежить тільки від її стану в сьогоденні (при
) залежить тільки від її стану в сьогоденні (при  ) і не залежить від того, коли і яким чином система прийшла в цей стан.
) і не залежить від того, коли і яким чином система прийшла в цей стан. , називається границя відношення ймовірності переходу із стану
, називається границя відношення ймовірності переходу із стану  в стан
в стан  за малий проміжок часу
за малий проміжок часу  , що примикає до моменту
, що примикає до моменту 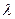 відповідних потоків подій. Якщо всі ці потоки найпростіші, то процес, що протікає в системі
відповідних потоків подій. Якщо всі ці потоки найпростіші, то процес, що протікає в системі  . Для опису випадкового процесу, що протікає в цій системі застосовуються, так звані, імовірності станів
. Для опису випадкового процесу, що протікає в цій системі застосовуються, так звані, імовірності станів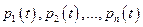 , (Б.2.1)
, (Б.2.1) ймовірність того, що система
ймовірність того, що система  ).
). виконується умова нормування
виконується умова нормування . (Б.2.2)
. (Б.2.2) . (Б.2.3)
. (Б.2.3) , потрібно задати початковий розподіл ймовірностей
, потрібно задати початковий розподіл ймовірностей , (Б.2.4)
, (Б.2.4) . (Б.2.5)
. (Б.2.5) , (Б.2.6)
, (Б.2.6)