|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расчёт цепей магнитного поля ⇐ ПредыдущаяСтр 8 из 8
Пример расчета разветвленной магнитной цепи методом 2-х узлов Для схем, содержащих только два узла или приводящихся к ним, применяют метод двух узлов. Пусть дана магнитная цепь (Рис.5.16):
Рис. 5.16
Кривая намагничивания стали дана в виде таблицы: Таблица 5.1
1 Найти магнитные потоки Ф1, Ф2 и Ф3 в ветвях магнитной цепи методом двух узлов. 2 Для принятых в п.I положительных направлений начальных потоков и заданного направления МДС составить систему уравнений по законам Кирхгоффа. Решение 1 Обозначим узловые точки схемы буквами d и k . Выберем положительные направления потоков Ф1, Ф2 и Ф3 к узлу d. 2 Построим вебер–амперные характеристики для трех стержней, то есть зависимости потоков Ф1, Ф2 и Ф3 от нападений магнитных напряжений Для построения вебер-амперных характеристик Так как Ф = В·S, то для каждого табличного значения магнитной индукции В кривой намагничивания вычисляем соответствующие значение магнитного потока Ф для каждого стержня, где – S площадь поперечного сечения соответствующего сердечника. Падение магнитного напряжения на участках из ферромагнитного материала равно Падение магнитного напряжения на неферромагнитном участке (в воздушном зазоре) Таким образом, вебер-амперная характеристика для первого стержня Таблица 5.2
Вебер-амперная характеристика для второго стержня
Таблица 5.3
Вебер-амперная характеристика для третьего стержня
Таблица 5.4
3 В одной координатной системе строим ВАХ трех стержней (Рис. 5.17): кривую
Рис. 5.17 4 Введем понятие магнитного напряжения, как разность магнитных потенциалов, между узлами d и k :
Выразим магнитный потенциал точки d (
где
Для второй ветви: Для третьей ветви: 5 Определение магнитных потоков в ветвях будем осуществлять графически (Рис. 5.18). 5.1 Начало кривой 1
Рис. 5.18 5.2 Из точки Восстановим в этой точке перпендикуляр к оси абсцисс. Ординаты точек пересечения перпендикуляра с кривыми 1',2',3' дадут соответственно потоки Поток Примечание.Если бы какая - либо МДС изменила направление на противоположное (в результате изменения направления протекания тока в этой обмотке ), то в уравнение для 6 При расчетах магнитных цепей, как и электрических, используют первый и второй законы Кирхгофа. Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю: Второй закон Кирхгофа; алгебраическая сумма падений магнитного напряжения вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль этого контура: Для написания уравнений по законам Кирхгофа следует произвольно выбрать положительные направления потоков в ветвях и положительные направления обхода контуров. Если направление магнитного потока на некотором участке совпадает с направлением обхода, то падение магнитного напряжения этого участка входит в сумму По законам Кирхгофа должно быть составлено столько уравнений, сколько ветвей в цепи (в данном случае нужно составить три уравнения, m=3) По первому закону Кирхгофа составляется (k-1) уравнение, где k количество узлов (k=2). По второму закону Кирхгофа следует ставить m-(k1)-уравнение, т.е. 3-(2-1)=2 уравнения. Для определения положительного направления МДС пользуются мнемоническим правилом: если сердечник мысленно охватить правой рукой, расположив ее пальцы по току в обмотке, а затем отогнуть большой палец, то последний укажет направление МДС. Учитывая вышеизложенное, составим систему уравнений для данной магнитной цепи: Узел d: Контур 1: Контур 2:
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 1 Евдокимов Ф.Е. Теоретические основы электротехники: учебник для техникумов/Ф.Е.Евдокимов: М.: Высшая школа, 1981. – 487с. 2 Данилов И.А. Общая электротехника с основами электроники: учебное пособие для техникумов /И.А. Данилов, П.М.Иванов. – М.: Высшая школа, 1989. – 752с. 3 Общая электротехника с основами электроники: учебник для техникумов / В.А.Гаврилюк., Б.С Гершунский., А.В.Ковальчук, Ю.А. Куницкий. – К.: Вища школа, 1980. - 480с. 4 Попов В.С. Общая электротехника с основами электроники: учебник для техникумов. / В.С. Попов, С.А Николаев. – М.: Энергия, 1997. - 568с. 5 Березкина Т.Ф. Задачник по общей электротехнике с основами электроники: учебное пособие для техникумов / Т.Ф. Березкина, Н.Г. Гусев, В.В. Масленников. – М.: Высшая школа, 1991. - 384с. 6 Белоусова Н.Б. Преподавание электротехники: методическое пособие/ Н.Б. Белоусова, О.В. Толчеев. – М.: Высшая школа, 1988. - 191с. 7 Евдокимов Ф.Е. Общая электротехника. Учебник для техникумов / Ф.Е. Евдокимов – М.: Высшая школа, 1987. – 352с.
Поиск по сайту: |




 и
и  соответственно.
соответственно. будем использовать кривую намагничивания стали
будем использовать кривую намагничивания стали  , заданную в виде таблицы 1.
, заданную в виде таблицы 1.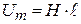 , где H – значение напряжённости поля, взятое из таблицы 1, l –длина сердечника.
, где H – значение напряжённости поля, взятое из таблицы 1, l –длина сердечника. , где
, где  - длина воздушного зазора.
- длина воздушного зазора. рассчитывается по формулам :
рассчитывается по формулам : ,
, 



 ,
, 


 :
: ,
, 

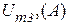
 - обозначим 1 , кривую
- обозначим 1 , кривую  - обозначим 2 и кривую
- обозначим 2 и кривую 

 ) через магнитный потенциал точки k (
) через магнитный потенциал точки k (  ), следуя от точки k к точке d, сначала по первой ветви, затем по второй и по третьей ветвям:
), следуя от точки k к точке d, сначала по первой ветви, затем по второй и по третьей ветвям: ,
,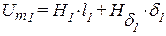 - падение магнитного напряжения по первой ветви. Знак минус обусловлен тем, что при перемещении согласно с направлением потока, магнитный потенциал понижается. При движении, встречном потоку, магнитный потенциал возрастает и необходимо ставить знак плюс. Перед I1W1 ставится знак плюс, так как при перемещении от k к d идем согласно с направлением МДС I1W1. Таким образом:
- падение магнитного напряжения по первой ветви. Знак минус обусловлен тем, что при перемещении согласно с направлением потока, магнитный потенциал понижается. При движении, встречном потоку, магнитный потенциал возрастает и необходимо ставить знак плюс. Перед I1W1 ставится знак плюс, так как при перемещении от k к d идем согласно с направлением МДС I1W1. Таким образом:
 , так как МДС в этой ветви отсутствует.
, так как МДС в этой ветви отсутствует. .
. смещаем в точку
смещаем в точку  A. Кривая 2
A. Кривая 2  A.
A.
 A возводим перпендикуляр и кривую 1 отображаем зеркально относительно этого перпендикуляра. Получаем кривую
A возводим перпендикуляр и кривую 1 отображаем зеркально относительно этого перпендикуляра. Получаем кривую  , подобным образом получаем кривую 3'. Характеристику
, подобным образом получаем кривую 3'. Характеристику  и обозначаем ее 4'. Точка m пересечения кривой 4' с осью абсцисс дает значение
и обозначаем ее 4'. Точка m пересечения кривой 4' с осью абсцисс дает значение  , при котором удовлетворяется уравнение:
, при котором удовлетворяется уравнение:  ,
,  .
. и
и  по величине и по знаку.
по величине и по знаку. оказался отрицательным. Это означает, что в действительности он направлен противоположно первоначально выбранному направлению.
оказался отрицательным. Это означает, что в действительности он направлен противоположно первоначально выбранному направлению. .
.

 со знаком плюс, если встречно ему, то со знаком минус. Аналогично, если МДС совпадает с направлением обхода, она входит в
со знаком плюс, если встречно ему, то со знаком минус. Аналогично, если МДС совпадает с направлением обхода, она входит в  со знаком плюс, в противном случае - со знаком минус. В данной схеме потоки направлены к узлу d, контуры будем обходить по часовой стрелке.
со знаком плюс, в противном случае - со знаком минус. В данной схеме потоки направлены к узлу d, контуры будем обходить по часовой стрелке.