Расчёт сложной электрической цепи

используя:

- метод непосредственного применения законов Кирхгофа;

- метод контурных токов;

- метод узловых потенциалов;

- метод эквивалентного генератора и т.д.

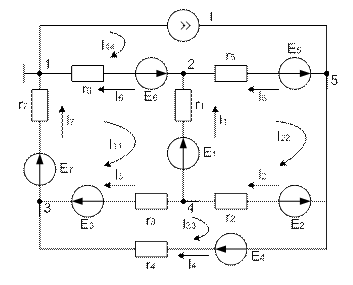
Пусть задана сложная электрическая цепь (Рис. 5.1).

Дано: r₁ = 20 Ом; Е₁ = 20 В;

r₂ = 30 Ом; Е₂ = 30 В;

r₃ = 40 Ом; Е₃ = 40 В;

r₄ = 50 Ом; Е₄ = 50 В;

r₅ = 60 Ом; Е₅ = 60 В;

r₆ = 70 Ом; Е₆ = 70 В;

r₇ = 80 Ом; Е₇ = 80 В;

r₈ = 90 Ом; Е₈ = 90 В;

I = 10А.

Рис. 5.1

Требуется:

1 Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях.

2 Определить токи во всех ветвях схемы методом контурных токов.

3 Используя токи, найденные при выполнении п.2, рассчитать потен- потенциалы узлов, применяя законы Ома и Кирхгофа.

4 Определить токи во всех ветвях схемы методом узловых потенциалов.

5 Используя потенциалы, найденные в п.3, определить токи во всех ветвях семы.

6 Составить баланс мощности в исходной схеме.

7 Определить ток I₁ в заданной схеме с источником тока, используя метод эквивалентного генератора.

8 Начертить потенциальную диаграмму для любого контура.

9 Определить показания вольтметра.

Решение

Метод непосредственного применения законов Кирхгофа

Необходимо преобразовать исходную схему так, чтобы источник тока находился во внешней цепи (Рис. 5.2).

Для решения данной задачи используются первый и второй законы Кирхгофа.

Методика расчёта:

1 Определяют число неизвестных токов и уравнений m. В данной цепи семь неизвестных токов, т.е. m = 7. Значит для однозначного решения такой задачи, как известно из алгебры, необходимо располагать семью линейно-независимыми уравнениями.

Рис. 5.2

2 Выбирают произвольное направление токов и обхода в контуре. Например, по часовой стрелке.

3 Записывают (k-1) уравнение по первому закону Кирхгофа, где k – количество узлов. Уравнение для оставшейся k-ой узловой точки уже будет следствием первых (k-1) уравнений, т.е. оно не будет независимым. Для нашей цепи k =5.

4 Недостающие m – (k –1) уравнения составляют по второму закону Кирхгофа. Чтобы все эти уравнения были независимыми, т.е. каждое не было следствием других, необходимо выбрать такие контуры для составления уравнений, чтобы каждый из них отличался от других, по меньшей мере, одним новым участком цепи (одной ветвью).

В данной схеме 4 независимых контура. При составлении уравнений по законам Кирхгофа нужно учитывать правило знаков, рассмотренное ранее.

Таким образом, для расчета токов во всех ветвях схемы составляется система из 7 уравнений: для узла 1: I₆+I₇ – I = 0;

для узла 2: I₁+I₅ – I₆ = 0;

для узла 3: I₃+I₄ – I₇ = 0;

для узла 4: I₂ – I₁ – I₃ = 0;

для контура I: –I₁r₁+I₃r₃+I₇r₇ – I₆ r₆ = -E₁+E₃+E₇+E₆;

для контура II: I₁r₁ – I₅r₅+I₂r₂ = E₁+E₅ – E₂;

для контура III: I₄I₄ – I₃I₃ – I₂I₂ = Е₂+Е₄ – Е₃.

Решение системы алгебраических уравнений относительно неизвестных токов и является решением поставленной задачи.

Если при решении появляются токи отрицательного значения, то для этих токов надо выбрать направление противоположное первоначально выбранному.

Метод контурных токов

Метод контурных токов по сравнению с предыдущим методом позволяет сократить количество составленных уравнений. В этом методе за неизвестные величины принимаются так называемые контурные токи, замыкающиеся в контурах.

Методика расчёта

1 Выбирают в схеме независимые контуры.

2 Для выбранных независимых контуров произвольно принимают нап- равления контурных токов в них. Для простоты решения направления контурных токов принимают совпадающими с направлением обхода контуров.

3 Составляют для выбранных контуров уравнения по второму закону Кирхгофа относительно контурных токов.

Для цепи, изображённой на рис. 5.2 можно выделить 4 независимых контура. Поскольку во внешней ветви четвертого контура находится источник тока I, величина которого известна I₄₄ = I = 10А, то уравнение для этого контура не оставляется. Таким образом, система будет состоять из 3-х уравнений.

В смежных сопротивлениях r_1, r_2, r_3, r_5, и r₆ контурные токи направлены

встречно, поэтому падения напряжения в этих резисторах определяются разностью этих токов. Если бы контурные токи в смежных сопротивлениях были бы направлены согласно, тогда падения напряжения в смежных резисторах определялись бы суммой контурных токов. Если источников ЭДС в контуре несколько, то источник ЭДС войдет в уравнение со знаком «плюс», если его направление совпадет с направлением обхода контура, если не совпадает, то нужно поставить знак «минус». Таким образом,:

I₁₁r₇ + (I₁₁ –I₄₄) r₆ + (I₁₁ –I₂₂) r₁ + (I₁₁ – I₃₃) r₃ = –E₁+E₃+E₇+E₆

(I₂₂ –I₄₄) r₅ + (I₂₂ –I₃₃) r₂ + (I₂₂ –I₁₁) r₁ = E₁+E₅ – E₂

I₃₃ r₄ + (I₃₃ –I₁₁) r₃ + (I₃₃ – I₂₂) r₂=E₂+E₄ – E₃ .

После преобразования получим следующую систему:

I₁₁ (r₁+ r₃+ r₆+ r₇)-I₂₂r₁ –I₃₃r₃ - I₄₄r₆= –E₁+E₃+E₇+E₆

I₂₂ (r₁ + r₂ + r₅)-I₁₁r₁ - I₃₃r₂ - I₄₄r₅ = E₁+E₅ – E₂

I₃₃ (r₂+ r₃ + r₄) - I₁₁r₃ - I₂₂r₂ = E₂+E₄ – E₃.

I₁₁ (20+40+70+80) – 20I₂₂ – 40I₃₃ – 10·70 = -20 + 40 + 80 + 70

I₂₂ (20+30+60) – 20I₁₁ – 30I₃₃ – 10·60 = 20 + 60 – 30

I₃₃ (30+40+50) – 40I₁₁ – 30I₂₂ = 30 + 50 – 40.

21I₁₁ – 2I₂₂ – 4I₃₃ = 87

-2I₁₁ + 11I₂₂ – 3I₃₃ = 65

-4I₁₁ – 3I₂₂ + 12I₃₃ = 4.

Решив систему, получим: I₁₁=5,73 (A), I₂₂=8,116 (A), I₃₃=4,272 (A).

4 В результате решения системы уравнений будут известны контурные токи I_1I, I₂₂ и I₃₃.От контурных токов необходимо перейти к токам в ветвях I₁,

I_2, I_3, I_4, I_5, I_6, I_7. В ветвях, не являющихся общими для смежных контуров, найденный контурный ток будет равен действительному току ветви. В ветвях же общих для смежных контуров действительный ток ветви равен алгебраической сумме контурных токов.

Таким образом:

I₁ =I₂₂ – I₁₁ = 8,116 – 5,73 =2,386 (A),

I₂ = I₂₂ – I₃₃ = 8,116 – 4,272 = 3,844 (A),

I₃ = I₁₁ – I₃₃ = 5,73 – 4,272 = 1,458 (A),

I₄ = I₃₃ = 4,272 (A),

I₅ = I – I₂₂ = 10 – 8,116 = 1,884 (A),

I₆ = I – I₁₁ = 10 – 5,73 = 4,27 (A),

I₇ = I₁₁ = 5,73 (A).

Поиск по сайту: