 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Explain the Hall effect. ⇐ ПредыдущаяСтр 10 из 10
The Hall effect is the production of a voltage difference (the Hall voltage) across anelectrical conductor, transverse to an electric current in the conductor and a magnetic field perpendicular to the current. It was discovered by Edwin Hall in 1879. The Hall coefficient is defined as the ratio of the induced electric field to the product of the current density and the applied magnetic field. It is a characteristic of the material from which the conductor is made, since its value depends on the type, number, and properties of the charge carriers that constitute the current. The Hall effect was discovered in 1879 by Edwin Herbert Hall while he was working on his doctoral degree at Johns Hopkins University in Baltimore, Maryland. His measurements of the tiny effect produced in the apparatus he used were an experimental tour de force, accomplished 18 years before the electron was discovered. The Hall effect is due to the nature of the current in a conductor. Current consists of the movement of many small charge carriers, typically electrons, holes, ions (see Electromigration) or all three. When a magnetic field is present that is not parallel to the direction of motion of moving charges, these charges experience a force, called the Lorentz force. When such a magnetic field is absent, the charges follow approximately straight, 'line of sight' paths between collisions with impurities, phonons, etc. However, when a magnetic field with a perpendicular component is applied, their paths between collisions are curved so that moving charges accumulate on one face of the material. This leaves equal and opposite charges exposed on the other face, where there is a scarcity of mobile charges. The result is an asymmetric distribution of charge density across the Hall element that is perpendicular to both the 'line of sight' path and the applied magnetic field. The separation of charge establishes an electric field that opposes the migration of further charge, so a steady electrical potential is established for as long as the charge is flowing. In the classical view, there are only electrons moving in the same average direction both in the case of electron or hole conductivity. This cannot explain the opposite sign of the Hall effect observed. The difference is that electrons in the upper bound of the valence band have opposite group velocity and wave vector direction when moving, which can be effectively treated as if positively charged particles (holes) moved in the opposite direction to that of the electrons.
Hall Effect measurement setup for electrons. Initially, the electrons follow the curved arrow, due to the magnetic force. At some distance from the current-introducing contacts, electrons pile up on the left side and deplete from the right side, which creates an electric field ξy. In steady-state, ξy will be strong enough to exactly cancel out the magnetic force, so that the electrons follow the straight arrow (dashed). For a simple metal where there is only one type of charge carrier(electrons) the Hall voltage VH is given by
where I is the current across the plate length, B is the magnetic field, t is the thickness of the plate, e is the elementary charge, and n is the charge carrier density of the carrier electrons. The Hall coefficient is defined as
where j is the current density of the carrier electrons, and
(The units of RH are usually expressed as m3/C, or Ω·cm/G, or other variants.) As a result, the Hall effect is very useful as a means to measure either the carrier density or the magnetic field. One very important feature of the Hall effect is that it differentiates between positive charges moving in one direction and negative charges moving in the opposite. The Hall effect offered the first real proof that electric currents in metals are carried by moving electrons, not by protons. The Hall effect also showed that in some substances (especially p-type semiconductors), it is more appropriate to think of the current as positive "holes" moving rather than negative electrons. A common source of confusion with the Hall Effect is that holes moving to the left are really electrons moving to the right, so one expects the same sign of the Hall coefficient for both electrons and holes. This confusion, however, can only be resolved by modern quantum mechanical theory of transport in solids. The sample inhomogeneity might result in spurious sign of the Hall effect, even in ideal van der Pauw configuration of electrodes. For example, positive Hall effect was observed in evidently n-type semiconductors. Another source of artifact, in uniform materials, occurs when the sample's aspect ratio is not long enough: the full Hall voltage only develops far away from the current-introducing contacts, since at the contacts the transverse voltage is shorted out to zero.
Поиск по сайту: |



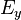 is the induced electric field. In SI units, this becomes
is the induced electric field. In SI units, this becomes