Unique Mechanical behavior of Ceramics and Glasses.

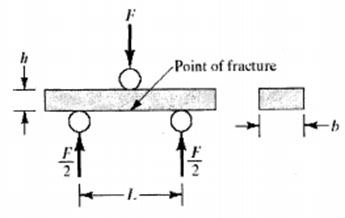
Many of the mechanical properties discussed for metals are equally important for ceramics and glasses used in structural applications. In addition, the different nature of these nonmetals leads to some unique mechanical behavior. Metal alloys generally demonstrate a significant amount of plastic deformation in a typical tensile test. In contrast, ceramics and glasses generally do not. This is an especially dramatic example of the fact that the ceramics are relatively weak in tension but relatively strong in compression. This behavior is shared by some cast irons and concrete. The strength parameter is the modulus of rupture, a value calculated from data in a bending test. The modulus of rupture (MOR) is given by MOR=3FL/(2bh² ) (1),

where F is the applied force, b, h and L are dimensions defined in Fig.1.

Modulus of rupture=MOR=3FL/(2bh² )

Fig.1. The bending test that generates a modulus of rupture. This strength parameter is similar in magnitude to a tensile strength. Fracture occurs along the outermost sample edge, which is under a tensile load.

Fig.2. Stress (σ_m) at the tip of a Griffith crack

The MOR is sometimes referred to as the flexural strength (F.S.) and is similar in magnitude to the tensile strength, as the failure mode in bending is tensile (along the outermost edge of the sample). The bending test, illustrated in Fig.1, is frequently easier to conduct on brittle materials than the traditional tensile test. One can note that υ for metals is typically ~1/3 and for ceramics ~1/4. To appreciate the reason for the mechanical behavior of structural ceramics, we must consider the stress concentration at a crack tips. For purely brittle material, the simple Griffith crack model is applicable. Griffith assumed that in any real material there would be numerous elliptical cracks at the surface and/or in the interior.

Since the crack tip radius can be as small as an intersification can be quite large. Routine production and handling of ceramics and glasses make Griffith flaws inevitable. Hence, these materials are relatively weak in tension. A compressive load tends to close, not open, the Griffith flaws and consequently does not diminish the inherent strength of the ionically and covalently bonded material. The drawing of small-diameter glass fibers in a controlled atmosphere is one way to avoid Griffith flaws. The resulting fibers can demonstrate tensile strengths approaching the theoretical atomic bond strength of the material. This helps to make them excellent reinforcing fibers for composite systems.

22. Mechanical behavior. Polymers. Tensile strength and modulus of elasticity.

Polymers

As with ceramics, the mechanical properties of polymers can be described with much of the vocabulary introduced for metals.

Tensile strengthand modulus of elasticityare important design parameters for polymers as well as inorganic structural materials.

MOR =3FL/2bh² (10), where F is the applied force, b, h and L are dimensions defined in Fig.6.10.

With the increased availability of engineering polymers for metals substitution, a greater emphasis has been placed on presenting the mechanical behavior of polymers in a format similar to that used for metals. Primary emphasis is on the stress-versus-strain data. Although strength and modulus values are important parameters for these materials, design applications frequently involve a bending,rather than tensile mode. As a result, flexural strength and flexural modulus are frequently quoted.As noted earlier, flexural strength (F.S.) is equivalent to the modulus of rupture defined for ceramics in Eq.10. and Fig. 6.10. For the same test specimen geometry, the flexural modulus, or modulus of elasticity in bending(E _flex), is

E _flex - L³m/4bh³ (12)

Where m is the slope of the tangentto the initial strain-line portion of the load-deflection curve and all other terms are defined relative to Fq. 10 and Fig. 6.10. An important advantageof the flexural modulus for polymersis that it describes the combined effects of compressive deformation (adjacent to the point of applied load in Fig. 6.10) and tensile deformation (on the opposite side of the specimen). For metals, as noted before, tensile and compressive moduli are generally the same. For many polymers, the tensile and compressive moduli differ significantly.

Modulus of rupture = MOR

= 3FL/(2bh²)

Fig. 6.10. The bending test that generates a modulus of rupture. This strength parameter is similar in magnitude to a tensile strength. Fracture occurs along the outermost sample edge, which is under a tensile load.

Some polymers, especially the elastomers,are used in structures for the purpose of isolation and absorption of shock and vibration. For such applications, a “dynamic” elastic modulusis more usefulto characterize the performance of the polymer under an oscillating mechanical load. For elastomers in general,the dynamic modulus is greater than the static modulus. For some compounds, the 2 moduli may differ by a factor of 2. The dynamic modulus of elasticity, E _dyn (in MPa), is E _dyn = Clf³ (13)

Where С is a constant dependent upon specific test geometry. I the moment of inertia(in kg m²) of the beam and weights used in the dynamic test, and f the frequency of vibration(in cycles/s) for the test. Eq. (13) holds for both compressive and shears measurements, with the constant С having a different value in each case. Typical stress-versus-strain curvesfor an engineering polymer, polyester looks similar to common stress-versus-strain plots for metals, there is a strong effect of temperature.On the other hand, this mechanical behavior is relatively independent of atmospheric moisture. Both polyester and acetal engineering polymers have these advantages. However, relative humidity is a design consideration for the use of nylons. There is the difference in elastic modulus(slope of the plots near the origin) for tensile and compressive loads. You can find some mechanical properties of the thermoplastic polymers (those that become soft and deformable upon-heating) in tables. Some table gives similar properties for the thermosetting polymers (those which become hard and rigid upon heating).

i®* Note,that the dynamic modulus values in the table are not,in general, greater than the tensile modulus values. The statement that the dynamic modulus of an elastomer is generally greater than the static modulus is valid for a given mode of stress application. The dynamic shear modulusvalue are, in general, greaterthan static shear modulus values.

23. Viscoelastic deformation. The glass transition temperature.

Поиск по сайту: