 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Exhibit relation between Point defects and solid – state diffusion.
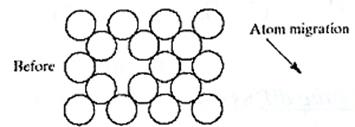
At sufficient temperatures, atoms and molecules can be quite mobile in both liquids and solids. Watching a drop of ink fall into a breaker of water and spread out until all the water is evenly colored gives a simple demonstration of diffusion, the movement of molecules from an area of higher concentration to an area of lower concentration. But diffusion is not restricted to different materials. At room temperature, H2O molecules in pure water are in continuous motion and migrating through the liquid as an example of self-diffusion. This atomic-scale motion is relatively rapid in liquids and relatively easy to visualize. It is more difficult to visualize diffusion in rigid solids. Nonetheless, diffusion does occur in the solid state. A primary difference between solid-state and liquid-state diffusion is the low rate of diffusion in solids. Looking back at the crystal structures, we can appreciate that diffusion of atoms or ions through those generally tight structures is difficult. In fact, the energy requirements to squeeze most atoms or ions through perfect crystal structures are so high as to make diffusion nearly impossible. To make solid-state diffusion practical, point defects are generally required. Fig.1 illustrates how atomic migration becomes possible without major crystal structure distortion by means of a vacancy migration mechanism. It is important to note that the overall direction of material flow is opposite to the direction of vacancy flow. occurs by a mechanism of vacancy migration. Note that the overall direction of material flow (the atom) is opposite to the direction of vacancy flow. Diffusion by an interstitialcy mechanism illustrates effectively the random walk nature of atomic migration. This randomness does not preclude the net flow of material when there is an overall variation in chemical composition. Although each atom of solid A has an equal probability of randomly "walking" in any direction, the higher initial concentration of A on the left side of the system will cause such random motion to produce interdiffusion, a net flow of A atoms into solid B. Similarly solid diffuses into solid A.
Fig.1. Atomic migration occurs by a mechanism of vacancy migration. Note that the overall direction of material flow (the atom) is opposite to the direction of vacancy flow. The formal mathematical treatment of such diffusional flow begins with an expression known as Fick's first law, Jx=-D(dc/dx)(1),where Jxis the flux, or flow rate, of the diffusing species in the x-direction due to a concentration gradient (dc/dx). D-proportionality coefficient (called the diffusion coefficient or, simply, the diffusivity). The geometry of Eq.(1) is illustrated in figure 1. The concentration gradient at a specific point along the diffusion path changes with time is t. This transient condition is represented by a second-order differential equation also known as Fick's second law, Fig.2.Geometry of Fick's first law For many practical problems, one can assume that D is independent of C, leading to a simplified version of Eq.(2):
Поиск по сайту: |

 (2)
(2) 
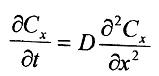 (3)
(3)